Theory
The inverse filtering is a restoration technique for deconvolution, i.e., when the image is blurred by a known lowpass filter, it is possible to recover the image by inverse filtering or generalized inverse filtering. However, inverse filtering is very sensitive to additive noise. The approach of reducing one degradation at a time allows us to develop a restoration algorithm for each type of degradation and simply combine them. The Wiener filtering executes an optimal tradeoff between inverse filtering and noise smoothing. It removes the additive noise and inverts the blurring simultaneously.
The Wiener filtering is optimal in terms of the mean square error. In other words, it minimizes the overall mean square error in the process of inverse filtering and noise smoothing. The Wiener filtering is a linear estimation of the original image. The approach is based on a stochastic framework. The orthogonality principle implies that the Wiener filter in Fourier domain can be expressed as follows:
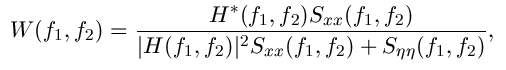
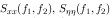are respectively
power spectra of the original image and the
additive noise, and
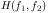is the blurring filter.
It is easy to see that the Wiener filter has two separate
part, an inverse filtering part and a noise smoothing part.
It not only performs the deconvolution by inverse filtering
(highpass filtering)
but also removes the noise with a compression operation (lowpass
filtering).
Implementation
To implement the Wiener filter in practice we have to estimate the power spectra of the original image and the additive noise. For white additive noise the power spectrum is equal to the variance of the noise. To estimate the power spectrum of the original image many methods can be used. A direct estimate is the periodogram estimate of the power spectrum computed from the observation:
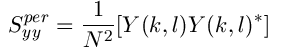
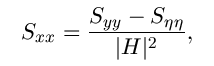
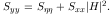The
power spectrum
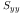can be estimated directly
from the observation using the periodogram estimate.
This estimate results in a cascade implementation
of inverse filtering and noise smoothing:
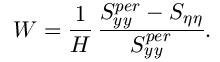
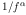model.
Experimental Result
To illustrate the Wiener filtering in image restoration we use the standard 256x256 Lena test image. We blur the image with the lowpass filter
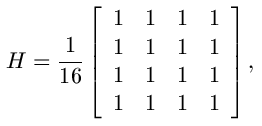
Test Image Lena and Blurred Image Lena
 |
 |
 | PSNR = Infinity, MSE = Zero |
PSNR = 23.2993, MSE = 304.1938 |
PSNR = 19.1447, MSE = 791.7906 |
Matlab Programs
-
inverseFilter.m
wienerFilter.m
wienerDriver.m