Theory
Although the Wiener filtering is the optimal tradeoff of inverse filtering and noise smoothing, in the case when the blurring filter is singular, the Wiener filtering actually amplify the noise. This suggests that a denoising step is needed to remove the amplified noise. Wavelet-based denoising scheme, a successful approach introduced recently by Donoho, provides a natural technique for this purpose. Therefore, the image restoration contains two separate steps: Fourier-domain inverse filtering and wavelet-domain image denoising. The digram is shown as follows.
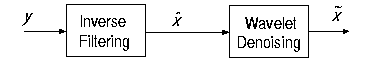
Donoho's approach for image restoration improves the performance, however, in the case when the blurring function is not invertible, the algorithm is not applicable. Furthermore, since the two steps are separate, there is no control over the overall performance of the restoration. Recently, R. Neelamani et al. proposed a wavelet-based deconvolution technique for ill-conditioned systems. The idea is simple: employ both Fourier-domain Wiener-like and wavelet-domain regularization. The regularized inverse filter is introduced by modifying the Wiener filter with a new-introduced parameter:
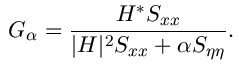
The parameter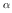 
can be optimally selected to minimize
the overall mean-square error. The diagram of the algorithm
is displayed as follows.
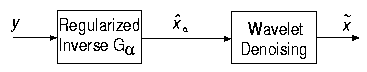
The implementation of the regularized inverse filter involves the estimation of the power spectrum of the original image in the spatial domain. Since wavelet transforms have good decorrelation property, the wavelet coefficients of the image can be better modeled in a stochastic model, and the power spectrum can be better estimated. This inspires a new approach: changing the order of the regularized inverse filtering and the wavelet transform. (See the following digram)
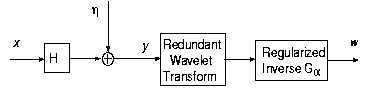
This way the both inverse filtering and noise smoothing can be performed in wavelet domain. Specifically, the power spectrum of the image in a same subband can be estimated under the assumption that the wavelet coefficients are independent. Therefore, the power spectrum is just the variance of the wavelet coefficients. We note that the exchange of the order of inverse filtering and wavelet transform is valid only when undecimated wavelet transform is used and the blurring function is separable. Therefore, for interpretation we can exchange the order of the blurring operation and the wavelet transform, which means that the inverse filtering cancels the blurring in the wavelet domain. So, wavelet thresholding results in a reasonable estimate. The above explanation can be visualized using the following figure.
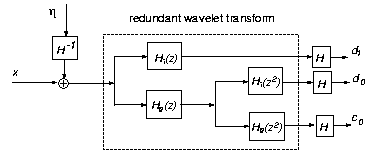
Simulation
As usual we corrupted the standard 256x256 lena test image by convolving wit the simple 4x4 square blurring filter
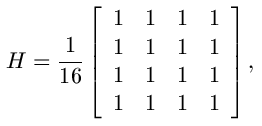
and adding zero-mean white Gaussian noise of variance 100.
The three introduced wavelet-based image restoration
algorithms are applied to the corrupted image, and the results are
reported in the following table. According to the
visual performance and the mean square error, the
algorithms improve the restoration performance.
However, the denoising step uses wavelet thresholding
to remove the noise, the images are blurred a little bit again,
although the MSE is improved.
Test Image Lena and Blurred Image Lena
 |
 | PSNR = 23.2993, MSE = 304.1938 |
PSNR = 16.8552, MSE = 1341.4 |
 |
 |
PSNR = 19.5115, MSE = 727.7 |
PSNR = 20.1223, MSE = 632.2 |
Matlab Programs
-
inverseFilter.m
wienerFilter.m
subbandFilter.m
waveletDriver.m