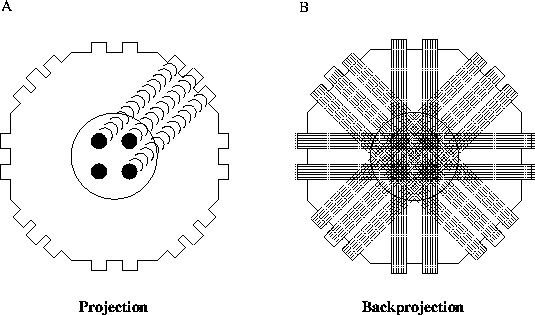
Figure 5: Illustration of back projection
Filtered backprojection as a concept is relatively easy to understand. Let's assume that we have a finite number of projections of an object which contains radioactive sources (Fig. 5 A). The projections of these sources at 45 degree intervals are represented on the sides of an octagon. Figure 5 B illustrates the basic idea behind back projection, which is to simply run the projections back through the image (hence the name ``back projection'') to obtain a rough approximation to the original. The projections will interact contstructively in regions that correspond to the emittive sources in the original image. A problem that is immediately apparent is the blurring (star-like artifacts) that occur in other parts of the reconstructed image. One would expect that a high-pass filter could be used to eliminate blurring, and that is the case. The optimal way to eliminate these patterns in the noiseless case is through a ramp filter [5]. The combination of back projection and ramp filtering is known as filtered back projection.

Figure 5: Illustration of back projection
For parallel beam tomography the projections can be expressed as the Radon
transform of the object that is to be reconstructed. The Radon transform is
defined as:
![]()
i.e., the line integral along a line (a tomography beam) at an angle
![]() from the y-axis and at a distance |s| from the origin. By
rotating the coordinate system,
from the y-axis and at a distance |s| from the origin. By
rotating the coordinate system,
![]()
or
![]()
![]() can be expressed as
can be expressed as