One approach for reconstructing the image is simply to take the inverse Radon transform of the projections. This involves two steps; the image is back projected and then filtered with a two dimensional ramp filter.
The back projection operator, 
is defined as
This operator represents the accumulation of the projections that pass through the point (x,y). As in the example above, the back projection is a blurred version of the desired image.
The image can be now unblurred with a two-dimensional ramp
filter. Because two-dimensional filtering is computationally
intensive, a better a better approach is to reverse the order of the
filtering and the back projection. Figure 6
illustrates both approaches. The second approach is possible due to
the projection slice theorem, which states that the one-dimensional
Fourier transform with respect to s of 
is equal to the
central slice at angle 
of the two-dimensional Fourier
transform of f(x,y),
The projection slice theorem implies that the Radon transform of the two-dimensional convolution of two functions is equal to the one-dimensional convolution of their Radon transforms. Convolution has the nice property of being symmetric, i.e f*g=g*f. This can be used to find a closed formula for the inverse Radon transform. It also implies a simpler inverse Radon scheme than before. It can be summarized with the following two points:
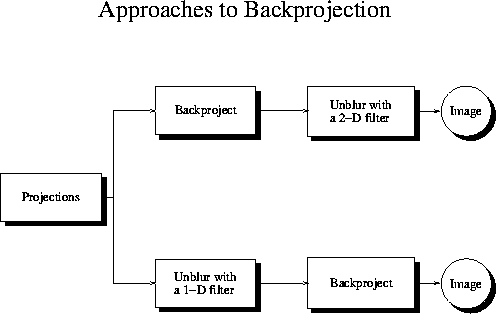
Figure 6: Illustration of the two possible cases for filtered
back projection. Most algorithms today does a one-dimensional filtering of the
projections before the back projection.
