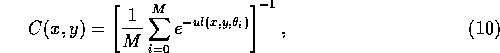
All real data will be corrupted in some way by attenuation. There are
several algorithms that compensate for this. These are usually
post-processing techniques that operate on the the output of the
filtered back projection. A very widely used method is Chang's
method, described in reference [2]. This method assumes
constant attenuation throughout the whole object. Each pixel
within the object of interest is simply multiplied by a correction
coefficient. These coefficients can be expressed as:
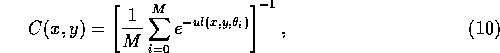
where 
is the distance that the projection i goes
through the attenuating material, M is the total number of
projections, and u is an attenuation factor, typically assumed to be
.11 
. C(x,y) will be based on the average of the attenuation
of all the projections that passes through the point.
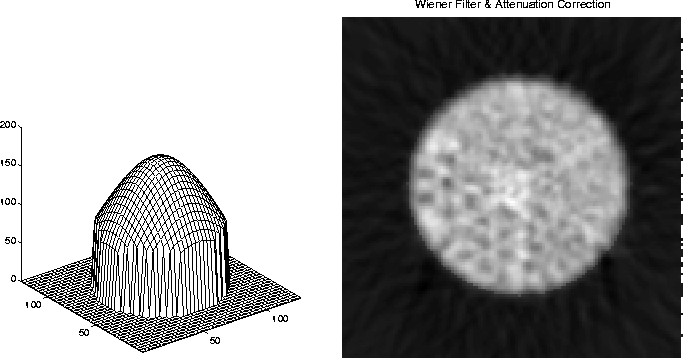
Figure 8: The left plot shows the mask that we apply to the
image to correct for attenuation. The right plot shows the
attenuation corrected image for the SPECT data.
The mask of all these correction coefficients is displayed in Fig. 8. It is customized for the SPECT data of the phantom, with circular symmetry. We calculated the attenuation correction only inside the circular region of interest, setting the mask to 1 outside that region. The right plot of Fig. 8 shows the image after attenuation correction. Compared to Fig. 7 we can see that the bright edges that exist in Fig. 7 now have disappeared. The intensity is more evenly distributed in this case. This correction factor must be calculated for each pixel (x,y), and the algorithm needs to go through three nested loops. As in the case of back projection, this problem can be formulated in matrix form, which will give us only one loop.
Our attenuation correction algorithm is specialized for the data that we have worked on. This data has circular symmetry with radius 42 and center at (67,66). A general algorithm would first find the edge of the attenuating object and then calculate the distance from the border of the object and the point. This could be accomplished using an edge detection or image segmentation scheme.