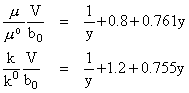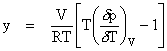For gases kcalc calls the ktpcalc program that is already in start301. This program is designed for light gases only as dense gases require a more complicated analysis.

The thermal conductivity for dense gases can be determined using the Enskog theory. By idealizing molecules as rigid spheres with diameter alpha(0) and taking low-pressure properties for viscosity ( m0 ) and thermal conductivity (k0 ) as constants the following relationships can be developed:

In these idealized relationships, V (molar volume) = and b(0) = *pi*N*alpha(0)^3 where N is Avogadro's number. The quantity y comes from the equation of state for rigid spheres:

Enskog further theorized that if one were to account for real gases instead of idealized rigid spheres, y can be empirically determined by:

Thus, in order to include dense gases in the kcalc program, alpha(0) needs to be determined and pressure must be included as a parameter. The pressure differential in the real gas empirical equation presented an additional challenge and would have required the entire kcalc program for gases (ktpcalc) to be rewritten to include pressure.

To verify that the kcalc can successfully call the ktpcalc program while in start301, we solved and example from the textbook.

Here are your compounds' formulae and names:
No. Formula Name
----------------------------------------
1 H2 hydrogen
2 O2 oxygen
3 CO2 carbon dioxide

>> kcalc(200,2,'g')

ans =

0.0182

Answer from book (pg. 269)
k=.01833 in units W/m/K

Clearly there is very good agreement.