[ Go to CENG301 Homepage | CENG301 Notes Table of Contents]
[Go to previous section: 3.2| Go
to next section: 3.4]
[ Go to CENG301 Homepage |
CENG301 Notes Table of Contents]
![]()
On page 1:
On this page:
- The Functions: setne, mixe, and showe
- Example 7.25 in Reklaitis: using mixe
The three programs (mixe, sepe,
and reacte) will accomplish both material and
energy balances for the three operating units: the mixer, separator,
and reactor. A splitter requires essentially no modifications over
what was used as split. Before executing these
programs, a global array ne must be set with the proper
shape. The shape of ne is S by C+3, where S is the number of streams
and C is the number of components. The first column of ne stores the
stream temperatures with units given in the global variable Tdeg as
('C', 'F', 'R' or 'K'). The second column contains information about
the states of the streams. A 0 stored in the second column indicates
that the stream is a solid, a 1 indicates that it is a liquid and a 2
indicates it is a vapor. The third column contains the total enthalpy
of the stream:
Start301 will set ne to a zero matrix of dimensions S by C+3. This is done after answering the prompt in start301:
Enter the number of streams:
An auxiliary function helps in setting one stream's information in
ne. The comments in this function, setne
are shown next:
>> help setne
setne: used to set stream properties in ne
function setne(s,i,t,NS,j)
Argument List:
Argument Gives
s the state of the stream: 'l' for liquid,
'v' for vapor, 's' for solid.
i the index of the stream.
t the stream temperature in units of Tdeg.
NS the compound molar flow rates (mols/time) for the
compounds with indices j in cnms.
If the last argument is omitted, all compounds are
assumed to be given in NS.
Compounds with indices not in j will be given flow
rates of 0.
See also ISETNER, ISETNEV
Ex. setne('v',2,25,[2 5.5],[2 4])
will set the flows of compounds 2 and 4 as 2 and 5.5 mol/time
respectively. The rest of the flows will be set to 0.
The first argument is a character vector that must start with 'l' for
a liquid, 'v' for a vapor stream or 's' for a solid. A single
character is sufficient to designate the state of the stream. The
next argument gives the index of the stream; the next its temperature
in the units specified by Tdeg and the fourth argument the
component flow rates. If there is a fifth argument, it gives the
indices of the compounds that you want to set. The rest of the
compound flow rates will then be set to zeros. The function sets all
C+3 values in the row of data for the stream. Note the use of the
global variables cnms (and all its data arrays) and
Tdeg by the function. They must be set before
setne is executed (the easiest way to do this is
with start301).
Remember that an illustration of either a mass or energy module can
be accessed by simply typing the prefix pic to each module
name.
The mixer function mixe has four arguments as
shown in the listing:
function hdif=mixe(s,t,in,out)
% mixe - Energy balance mixer module
% function hdif=mixe(s,t,in,out)
% Argument List
% Argument Gives
% s the state of the exit stream:
% 'v' for vapor, 'l' for liquid, 's' for solid.
% t the temperature of the exit stream in Tdeg.
% in the indices of inlet streams,
% out the index of exit stream.
% hdif: the answer is the enthalpy out
% - the sum of the enthalpies in.
% Ex. mixe('v',55,[2 3 4],6)
% will mix streams 2, 3 and 4 to form stream 6.
% Stream 6 will be a vapor at 55Tdeg.
% For additional help and picture, see picmixe
% OKB, TYLC
global ne nc
if length(in)<2
ns=ne(in,4:(nc+3));
else
ns=sum(ne(in,4:(nc+3)));
end
j=find(ns);
setne(s,out,t,ns(j),j)
hdif=ne(out,3)-sum(ne(in,3));
The first line after the comments sets the names of global variables
used in the program. The next five lines of code determine where the
inlet flow rates are stored in ne and sums them to find the
component flows in the exit stream. The next line determines which of
the exit flows are non-zero so that in the fifth line, we can avoid
enthalpy calculations for missing components. The last line finds the
difference between the exit and the inlet enthalpies.
The image of mixe is here:
To illustrate the operation of
mixe with setne, we will use them
to do Example 7.25 on p. 463 of the text. First, set the
names of the four compounds: C6H6, C6H5CH3, CH4 and H2 and specify
the number of streams for ne with the
start301 program. Then our solution of the problem
will follow from:
Here are your compounds' formulae and names:
No. Formula Name ---------------------------------------- 1 C6H6 benzene 2 C6H5CH3 toluene 3 CH4 methane 4 H2 hydrogen Enter the number of streams: 3 >> Tdeg Tdeg = C >> setne ('v',2,400,[400 300 100 200]) <-- Setting stream 2 >> setne(' l',1,20,200,1) <-- Setting stream 1 for a flow of benzene = 200 mol/hr >> mixe('v',200,1:2,3) <-- Mixing ans = -1.5080e+04 <-- The required heat in kJ. needed to be removed >> showe(1:2,3,10,3) Inlet | Outlet Stream 1 2 Total | 3 Tmp C 20.00 400.00 | 200.00 State liquid vapor | vapor Entlpy 9817.8 82532.3 92350.2 | 77270.1 Compound Stream Flows benzene 200.000 400.000 600.000 | 600.000 toluene 0.000 300.000 300.000 | 300.000 methane 0.000 100.000 100.000 | 100.000 hydrogen 0.000 200.000 200.000 | 200.000 Total 200.000 1000.000 1200.000 | 1200.000
The function showe is used to
display the results in a readable form. It is quite short so we can
list all of it:

Note that it is short since most of the work is done by the much
longer function: dsplaye. The arguments are
identical to those with showm. If you wish to peruse
the longer function dsplaye, feel free to do so, but
you will find that it is the most complicated function in the
~ceng301/matlab/utilities directory. The first
argument of showe gives the inlet streams, the
second gives the exit streams. The last two arguments set the format
for printing flow rates.
>> 77270.1-92350.2 <-- This is the value returned by mixe:
ans = enthalpy out - enthaply in
-1.5080e+04
>> type ex725 <-- A function used to find the flow that
will give adiabatic mixing
function er=ex725(Nbenz)
setne('l',1,20,Nbenz,1)
er=mixe('v',200,1:2,3);
>> ex725(200) <-- this agrees with what we got for a flow
ans = of 200 before.
-1.5080e+04
>> ex725(500) <-- this gives a positive error. There must
ans = be some flow between 200 and 500 that is
699.0108 adiabatic
>> ssec2([200 500],'ex725(x)')
ans =
486.7101 <-- The text finds 486.7 kgmol/hr
>> showe(1:2,3,10,3)
Inlet | Outlet
Stream 1 2 Total | 3
Tmp C 20.00 400.00 | 200.00
State liquid vapor | vapor
Entlpy 23892.2 82532.3 106424.6 | 106424.6 <-- enthalpy in =
Compound Stream Flows enthalpy out
benzene 486.710 400.000 886.710 | 886.710
toluene 0.000 300.000 300.000 | 300.000
methane 0.000 100.000 100.000 | 100.000
hydrogen 0.000 200.000 200.000 | 200.000
Total 486.710 1000.000 1486.710 | 1486.710
Since our data bank has lots of missing data, there are many cases where the computer will generate meaningless enthalpies for compounds. You should always remember that each stream must be a single phase. If some of the compounds in the system being analyzed do not have data that allows us to determine their enthalpies in that phase, then we must avoid telling our programs to include them. The energy modules, try to help with this by determining which compounds in the exit stream(s) have zero flow rates. The modules then call the functions HinkJ and setne with last arguments that will get them to avoid the compounds that are missing. You may have to follow this same procedure. Here is a session to show how this can be done in calling setne. We have two streams and three compounds: CO2, O2 and C. The first stream has just C in it and the second one has CO2 and O2. If we try (after the start301 programs):
<-- Select Celsius for temperature units Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 CO2 carbon dioxide 2 O2 oxygen 3 C carbon Enter the number of streams: 2 >> setne('s',1,350,[0 0 50]) >> setne('v',2,300,[0 50 0]) >> setne('v',3,500,[50 0 0]) >> showe(1:2,3,10,2) Inlet | Outlet Stream 1 2 Total | 3 Tmp C 350.00 300.00 | 500.00 State solid vapor | vapor Entlpy NaN NaN NaN | NaN <-- Note NaNs Compound Stream Flows carbon dioxide 0.00 0.00 0.00 | 50.00 oxygen 0.00 50.00 50.00 | 0.00 carbon 50.00 0.00 50.00 | 0.00 Total 50.00 50.00 100.00 | 50.00
The programs are happy, but we do not get usable values for the
enthalpies of the streams. A better procedure in using
setne is:
>> setne('s',1,350,50,3)
>> setne('v',2,300,50,2)
>> setne('v',3,500,50, 1)
>> showe(1:2,3,10,2)
Inlet | Outlet
Stream 1 2 Total | 3
Tmp C 350.00 300.00 | 500.00
State solid vapor | vapor
Entlpy 218.40 419.37 637.78 | -18604.21
Compound Stream Flows
carbon dioxide 0.00 0.00 0.00 | 50.00
oxygen 0.00 50.00 50.00 | 0.00
carbon 50.00 0.00 50.00 | 0.00
Total 50.00 50.00 100.00 | 50.00
>>
The separator function operates in an analogous manner to the
mixer. The user must specify not only the fraction of each compound
that goes to the top stream but the temperature and state of each
exit stream. A listing of the function sepe is shown
next:
function hdif=sepe(stop,sbot,ttop,tbot,in,out,t)
% sepe: energy-balance separator module
% function hdif=sepe(stop,sbot,ttop,tbot,in,out,t)
% Argument List:
% Argument Gives
% stop state of the top stream: 'v', 'l', or 's'.
% sbot state of the bottom stream.
% ttop the temperature of the top stream in Tdeg.
% tbot the temperature of the bottom stream in Tdeg.
% in the index of feed,
% out the indices of the top and bottom streams
% in that order.
% t the fraction of each compound in the feed
% that goes to the top stream.
% sepe returns the sum of the enthalpies of the exit
% streams minus the enthalpy of the feed stream.
% Ex. sepe('v','l',120,150,2,[3 5],[.9 .35])
% might simulate a fractionator with stream 2 as the
% feed, 3 as the top product and 5 as the bottom.
% The top comes off as a vapor at 120Tdeg and gets
% 90% of the first component and 35% of the second.
% For additional help and picture, see PICSEPE
% OKB, TYLC
global ne nc
NS=ne(in,4:nc+3);
NST=NS.*t;
jt=find(NST);
NSB=NS-NST;
jb=find(NSB);
setne(stop,out(1),ttop,NST(jt),jt)
setne(sbot,out(2),tbot,NSB(jb),jb)
hdif=sum(ne(out,3))-ne(in,3);
The first line of code defines globals used by the function. The next
line extracts the feed flow rates into the vector NS and
puts the flows for the top exit stream in NST. The vector
jt stores the indices of the non-zero flow rates in this top
stream. The next two lines put the flows for the bottom stream in
NSB and the indices of non-zero flows in jb. The
function setne is used to set all the flow and state
conditions for the exit streams. Finally, the last line determines
and returns the difference between the enthalpies out and into the
separator.
This is an image of sepe:
Fig. 3.3.1 Energy Balance Separator: sepe
A more general version of the separator module is called
sepen. It allows you to have multiple inlet and as
many exit streams as you want. Do a help in MATLAB for more
information.
The following problem may be readily solved with this separator
function. Fifty mols of benzene and toluene at 360K are separated
into a top stream that has 95% of the benzene and 5% of the toluene.
The top stream exits as a vapor at the normal boiling point of
benzene and the bottom stream exits as a liquid at the normal boiling
point of toluene. Find the net heat required for this separation.
|
|
The simulator solution with sepe follows (after
start301 was used to specify the two compounds,
choosing Kelvin for temperature:
Input the name of your new file: test2
The output file name is: test2
Here are your compounds' formulae and names:
No. Formula Name
----------------------------------------
1 C6H6 benzene
2 C6H5CH3 toluene
Enter the number of streams: 3
>> Tdeg
Tdeg =
K
>> ts=TbpK
ts =
353.2610
383.7860
>> setne('l',1,360,[50 50]) <-- Setting stream 1
>> sepe('v','l',ts(1),ts(2),1,2:3,[.95,.05]) <-- Using sepe
ans =
1.7100e+03 <-- The heat required in kJ
>> showe(1,2:3,10,3)
Inlet | Outlet
Stream 1 | 2 3 Total
Tmp K 360.00 | 353.26 383.79
State liquid | vapor liquid
Entlpy 4028.0 | 4315.3 1422.7 5738.0
Compound Stream Flows
benzene 50.000 | 47.500 2.500 50.000
toluene 50.000 | 2.500 47.500 50.000
Total 100.000 | 50.000 50.000 100.000
The function sepen allows the user
to have multiple inlet and exit streams in a separator. It's help
code says:
Sepen: General purpose separator module
function hdif=sepen(s,tmp,in,out,t)
General purpose separator module:
The number of inlet and exit streams can be any integer >0.
Argument List:
Argument Gives
s vector of states of the exit stream(s).
('v', 'l', or 's')
tmp temperatures of exit streams in Tdeg.
in the indices of the inlet stream(s).
out the indices of the exit stream(s).
t The fraction of each compound in the product
that goes into each stream, except that the
last stream need not be given. Each row should
correspond to one exit stream. If tmp and out
are scalars, t does not need to be given.
sepen returns the sum of the enthalpies of the
exit streams minus the sum of the enthalpies
of the inlet streams.
Example 7.22 in Reklaitis illustrates the use of this program.
|
|
The program start301 is used to create the data file E7.22 with data for oxygen and benzene in it. After choosing a New Session, use Energy & Mass Balances in CENG 301's database, using Celsius as the temperature unit.
Input the name of your new file: E7.22 Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 O2 oxygen 2 C6H6 benzene Enter the number of streams: 4 >> Tdeg Tdeg = C
If we had made a mistake and set the temperature as Kelvin, we can easily change the value stored in Tdeg with the following command line:
>> Tdeg='C';
Set the flow in feed stream 1 using one hour of flow as the
basis:
>> setne('v',1,25,100000,1)
Write a simple program to give the error from mixing the two
streams and separating them as in the heat exchanger:
function er=ex722(FB)
global mw
% The flow of benzene is FB kg/hr, it's temperature is 250C.
setne('v',2,250,FB*1000/mw(2),2)
% The benzene out of the exchanger is saturated at 5.5bar or 550 kPa.
t4=teql(550);
% Stream 3 is a vapor at 200C, stream 4 is a liquid at t4(2)
% All the O2 goes into stream 3, none of the benzene goes into that stream.
er=sepen('vl',[200, t4(2)],1:2,3:4,[1 0]);
find a range in which there is a sign change:
>> ex722(100) ans = 4.7360e+05 >> ex722(2000) ans = -5.2541e+05
Use ssec2 to find the required amount of
benzene:
>> ssec2([100 2000],'ex722(x)') ans = 1.0007e+03
That's close to the value of 1050 kg/hr found in the text. Here is
what all the streams look like:
>> showe(1:2,3:4,9,0)
Inlet | Outlet
Stream 1 2 Total | 3 4 Total
Tmp C 25.00 250.00 | 200.00 147.05
State vapor vapor | vapor liquid
Entlpy 0 1390323 1390323 | 526178 864145 1390323
Compound Stream Flows
oxygen 100000 0 100000 | 100000 0 100000
benzene 0 12811 12811 | 0 12811 12811
Total 100000 12811 112811 | 100000 12811 112811
Here is the data found by use of sepen with the
trial and error function: ssec2 shown on the flow
diagram for the example:
|
|
The flow direction of the benzene has been reversed in this
picture since it would certainly require counter current flow in the
exchanger to have heat transfer from the benzene to the oxygen at all
points.
Note that sepen can be used with any number of inlet
and exit streams, it is not limited to just two of each as in this
example.
The function splite can be used in two ways. The
simple splitting operation requires no energy balance since each
outlet from the splitter has the same state, temperature, and
mass/mole fractions as the feed. For this case
splite does the same thing as
split, except the state and temperature in
ne are kept.
A picture of splite: Help on
splite gives:
>> help splite
splite: energy-balance splitter module
function hdif=splite(t,in,out,s,tmp)
Argument List
Argument Gives
t the fraction of the inlet stream
that goes to each exit stream.
in the index of the inlet stream.
out the indices of the exit streams.
s the states of the exit streams.
tmp the temperatures of the exit streams.
The last two arguments are optional. Without them this works as a
normal splitter. With them splite can be used as a sort of heat
exchanger on the exit streams.
Ex: splite([.2 .2 .2 .2 .2],1,2:6)
would split stream 1 into 5 equal parts in streams 2 through 6,
all with the same state and temperature as stream 1.
Ex: splite([.2 .3 .5],1,2:4,'vvl',[400 300 200])
would split stream 1 into streams 2, 3 and 4.
Stream 2 would get 20% of the flow, as a vapor at 400 Tdeg,
stream 3 would get 30% as vapor at 300 Tdeg,
and stream 4 would get the remaining 50% as liquid at 200 Tdeg.
Splite returns the enthalpy difference between the inlet and outlet
streams, which should be zero unless the last two arguments are given.
For additional help and picture of Ex. #2 , see PICSPLITE
JWD, TYLC
The function reacte simulates the behavior of a
reactor and computes material and energy balances for the process.
Before executing reacte, the arrays ne,
Tdeg, cnms as well as the stoic array for
the reactions must be set. A listing of reacte is
shown below:
function hdif=reacte(s,tmp,in,out,rs)
% Reacte: basic energy-balance reactor module (only one exit stream)
% function hdif=reacte(s,tmp,in,out,rs)
% Basic reactor module that includes an energy balance,
% only one exit stream is allowed.
% Argument List:
% Argument Gives
% s state of the exit stream: 'v', 'l', or 's'
% tmp temperature of exit stream in Tdeg.
% in the indices of the inlet streams!
% out the index of the exit stream.
% rs the reaction rates.
% reacte returns the enthalpy of the
% exit stream minus the sum of the enthalpies
% of the inlet streams.
% EX: reacte('v',920,[1 2],3,0.225);
% For additional help and picture see PICREACTE
% JWD, SHD & OKB, TYLC
global ne stoic
sne=size(ne);
nc=sne(2)-3;
NS=sum([ne(in,4:(nc+3));zeros(1,nc)]);
nout=NS+(rs*stoic);
j=find(abs(nout)>eps);
setne(s,out,tmp,nout(j),j)
hdif=ne(out,3)-sum(ne(in,3));
The first three lines of code sums the inlet flows (if there is more than one inlet stream) and puts the result into NS . It then uses a matrix multiply to find the effect of the reactions on these flows to produce the outlet flow rates. The vector, j, indicates the indices of the non-zero flow compounds in the exit stream. The function setne is then called to set the outlet flows and other data and the difference between the exit and inlet enthalpies returned in hdif.
The graphic for reacte
We will work the example problem 8.6 in the text to
illustrate reacte. At the same time, we will show
why the three functions were defined to return the net heat input to
the unit.
|
|
First we need to set the arrays cnms, stoic and Tdeg and then initialize ne. Execute start301 to specify the five compounds:
Input the name of your new file:noreact Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 NH3 ammonia 2 O2 oxygen 3 NO nitric oxide 4 H2O water 5 N2 nitrogen Here are your reactions: ---------------------------------------- 1) 4NH3 + 5O2 --> 4NO + 6H2O Enter the number of streams: 3 >> Tdeg='C'; <-- Working in °C
Next we can set the known flow streams:
>> setne('v',1,750,2.4*[1,79/21],[2 5]) <-- The air in 1
>> setne('v',2,25,1,1) <-- The ammonia in 2
Now react the two streams for a given exit temperature and
conversion:
>> reacte('v',920,[1 2],3,.225) <-- Reacting 1 and 2
ans =
-94.8887 <-- Reactor Result
>> showe(1:2,3,10,5)
Inlet | Outlet
Stream 1 2 Total | 3
Tmp C 750.00 25.00 | 920.00
State vapor vapor | vapor
Entlpy 257.057 -45.690 211.367 | 116.478
Compound Stream Flows
ammonia 0.00000 1.00000 1.00000 | 0.10000
oxygen 2.40000 0.00000 2.40000 | 1.27500
nitric oxide 0.00000 0.00000 0.00000 | 0.90000
water 0.00000 0.00000 0.00000 | 1.35000
nitrogen 9.02857 0.00000 9.02857 | 9.02857
Total 11.42857 1.00000 12.42857 | 12.65357
Note that our answer is returned by reacte as a negative 94.88 kJ per mol of NH3 added to the reactor. This is the same as 22.68 kcal/mol NH3 removed from the reactor and may be compared with 22.53 kcal/mol NH3 found in the text.
From convu:
94.88000 kJ/(mol) = 22.67727 kcal/(mol)
Note that even reacte forces you
to have a single exit stream. If your reactor has two or more product
streams, you must use a combination of reacte
followed by one or more uses of sepe. This is what
reacten does. Since the sepe module
can handle two exit streams with different states, this makes the
modules capable of handling all the common cases that you want.
Again, the help explains how reacten is different
from the other reactors.
>> help reacten
function hdif=reacten(s,tmp,in,out,rs,t)
General purpose reactor module:
The number of inlet and exit streams can be any integer >0.
Argument List:
Argument Gives
s vector of states of the exit stream(s).
('v', 'l', or 's')
tmp temperatures of exit streams in Tdeg.
in the indices of the inlet stream(s).
out the indices of the exit stream(s).
rs the reaction rates.
t The fraction of each compound in the product
that goes into each stream, except that the
last stream need not be given. Each row should
correspond to one exit stream. If tmp and out
are scalars, t does not need to be given.
reacten returns the sum of the enthalpies of the
exit streams minus the sum of the enthalpies
of the inlet streams.
Ex: reacten('vs',[312 25],1:2,3:4,[.94 0.21],[1 1 0]);
JWD, SHD & OKB, TYLC
This is the picture of reacten:
Example 8.4 in the Reklaitis text illustrates both the use of reacten and the way in which data for missing compounds may be inserted into the user's data bank with the program addcomp. The compound benzaldehyde is not among the compounds currently stored in the ceng301 data bank so we need to add information about it.
>> stdat2=addcomp Choose a database to edit <-- brings up the menu
We choose 301 Mass & Energy Balance and see next the very long menu
<-- Our choice from the first menu is 301 Mass & Energy Balance
 We
can enter as much data as we need into this the new data bank from
this menu. From the statement of the example problem we know or can
find by changing units the following:
We
can enter as much data as we need into this the new data bank from
this menu. From the statement of the example problem we know or can
find by changing units the following:
|
|
|
|
|
|
Name |
cnms |
benzaldehyde |
|
|
Formula |
form |
C6H5CHO |
|
|
Molecular Weight |
mw |
106.124 |
|
|
Latent Heat of Vaporization at normal boiling point |
LhlvkJ |
kJ/mol |
38.39 |
|
Normal Boiling Point |
TbpK |
K |
452.15 |
|
State of compound used in setting its "Standard" Heat of Formation |
Ststdh |
1 meaning liquid |
|
|
"Standard" Heat of Formation |
StdhkJ |
kJ/mol |
0 assumed and to be found |
|
Coefficients in polynomial giving the Specific Heat of Liquid |
cpl |
J/mol/K |
[189.86 0 0 0] |
|
Coefficients in polynomial giving the Specific Heat of Vapor |
cpv |
J/mol/K |
[129.7 0 0 0 0] |
To input each type of data, we click on the button with the array name we want. If we start with: For example to enter the compound name, we click on the cnms button and get the following message and give the name:
cnms= ? benzaldehyde
Then follow it by clicking on the appropriate buttons and entering all the data in the table as follows:
form= ? C6H5CHO Give a vector of length 1 mw= ? 106.124 Give a vector of length 1 LhlvkJ= ? 38.39 Give a vector of length 1 StStdh= ? 1 Give a vector of length 1 StdhkJ= ? 0 Give a vector of length 1 TbpK= ? 452.15 Give a vector of length 4 cpl= ? [189.86 0 0 0 ] Give a vector of length 5 cpv= ? [129.7 0 0 0 0]
When we click on the Finished button we will see:
stdat2= 1x135 struct array with fields: cnms ... ... dHComb
We need to save the augmented structure for use in start301.
>> save ex84 >> start301 Then choose from the next menu: New Session and then: Energy & Mass Balances and then: Your own Enter the name of your database: ex84 Which units do you want to use for temperature? Choose the temperature unit: Celcius Input the name for a new file or just hit a return: Input the number of compounds: 5 The number of compounds is: 5 Enter the name of compound # 1: C6H5CHO <-- This data base knows about benzaldehyde.
We can continue with a normal 301 session to set the other four compounds and the reactions until we see:
Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 C6H5CHO benzaldehyde 2 C6H5CH3 toluene 3 O2 oxygen 4 H2O water 5 CO2 carbon dioxide Here are your reactions: ---------------------------------------- 1) C6H5CH3 + O2 --> C6H5CHO + H2O <-- reaction we want the dH for 2) C6H5CHO + 8O2 --> 3H2O + 7CO2 <-- reaction we know the heat of combustion for >> intcp <-- we need to use this to set up icpl and icpv >> sethcp <-- this then sets the hcpl and hcpv vectors >> StdhkJ StdhkJ = 0 <-- The value for this is what we need to find first using the given 50.0000 heat of combustion for the compound at 18C 0 -241.8300 -393.5000
The heat of combustion for benzaldehyde is given at 18°C. This is the difference between the enthalpies of the products and the enthalpies of the feed to a reactor. We have to be careful to specify the state of the compounds as seen in the stoichiometric equation that defines the heat of reaction. In Example 8.4 this reaction is given as:
C6H5CHO(l) + 8O2(g) --> 3H2O(l) + 7CO2(g)
Thus we will set one mol of benzaldehyde as a liquid in stream 1 and 8 mols of oxygen in stream 2 as a gas. Then if we react all of them by a unit amount of reaction 2 to produce one stream with liquid water and one with vapor carbon dioxide, we will be carrying out the reaction as specified.
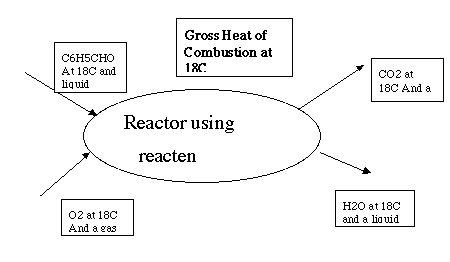
>> setne('l',1,18,1,1) <-- one mol of liquid benzaldehyde at 18C in stream 1
>> setne('v',2,18,8,3) <-- 8 mols of vapor O2 at 18C in stream 2
>> reacten('vl',[18 18], 1:2,3:4,[0 1],[1 1 1 0 1]) <-- vapor at 18C in stream 3
ans = liquid water at 18C in stream 4, 0 rxn 1, 1 rxn 2
-3.6118e+03 <-- calc. heat of rxn 2 using 0 for St dH liq benzaldehyde
841.3000 kcal/(mol) = 3519.937 kJ/(mol) <-- heat of rxn 2 given in the example
>> ans + 3519.937
ans =
-91.8504 <-- required Heat of Formation of banzaldehyde
22.11000 kcal/(mol) = 92.50659 kJ/(mol) <-- from the text
>> StdhkJ(1)=-91.8504 <-- replacing the 0 in StdhkJ(1)
StdhkJ =
-91.8504
50.0000
0
-241.8300
-393.5000
Now let's check to see that reacten really gives the heat of combustion given in the example.
>> sethcp <-- using the new value of the heat of formation in the hcp vectors
>> setne('l',1,18,1,1) <-- recalculating the enthalpy of stream 1
>> reacten('vl',[18 18], 1:2,3:4,[0 1],[1 1 1 0 1]) <-- executing reacten again
ans =
-3.5199e+03 <-- This now agrees with the given heat of combustion
>> showe(1:2,3:4,10,3) <-- Making sure that we carried out the combustion
Inlet | Outlet reaction
Stream 1 2 Total | 3 4 Total
Tmp C 18.00 18.00 | 18.00 18.00
State liquid vapor | vapor liquid
Entlpy -93.2 -1.6 -94.8 | -2756.3 -858.5 -3614.8
Compound Stream Flows
benzaldehyde 1.000 0.000 1.000 | 0.000 0.000 0.000
oxygen 0.000 8.000 8.000 | 0.000 0.000 0.000
water 0.000 0.000 0.000 | 0.000 3.000 3.000
carbon dioxide 0.000 0.000 0.000 | 7.000 0.000 7.000
Total 1.000 8.000 9.000 | 7.000 3.000 10.000
Turning attention to finding the heat of the first reaction at 25C. It was specified as:
C6H5CH3(g) + O2(g) --> C6H5CHO(g) + H2O(g)
>> setne('v',1,25,[1 1],2:3) <-- one mol each of vapor toluene & O2 in stream 1
>> reacte('v',25,1,2,[1 0]) <-- reacting all of the O2 and toluene to form vapor
ans = products
-336.0258 <-- The heat of reaction in kJ/mol
>> showe(1,2,12,3) <-- Making sure we carried out the reaction as
Inlet | Outlet specified
Stream 1 | 2
Tmp C 25.00 | 25.00
State vapor | vapor
Entlpy 50.0 | -286.0
Compound Stream Flows
benzaldehyde 0.000 | 1.000
toluene 1.000 | 0.000
oxygen 1.000 | 0.000
water 0.000 | 1.000
Total 2.000 | 2.000
336.0258 kJ/(mol) = 80.31352 kcal/(mol) <-- the text reports the value: 56.56
A corrected sign error in the book shows they should have found 80.46. We can show the agreement with the book is excellent except for the last value of the heat of reaction.
>> HinkJ(25,'v',1)-HinkJ(25,'l',1) <-- latent heat of benzaldehyde at 25C ans = 47.6546 47.65460 kJ/(mol) = 11.38993 kcal/(mol) <-- text: 11.4 >> HinkJ(25,'v',1) <-- heat of formation of benzaldehyde vapor at 25C ans = is exactly what HinkJ gives us. -44.1958 44.19580 kJ/(mol) = 10.56324 kcal/(mol) <-- text: 10.71
Note that while reacten could be used with any
separation, normally the separation will just be used to separate
compounds with different states into separate streams. Here is an
example of solving problem 8.28 in Reklaitis.
|
|
Basis: 100 mols air in stream 1.
Reactions:
1) CaCO3(s) --> CaO(s) + CO2(g)
2) C(s) + O2(g) --> CO2(g)
With N4 as the molar flow in stream 4 (the product lime stream)
we can set balances in all streams as:
Inlet Exit
Compound/Stream 1 2 3 4
1 O2 - 21 - -
2 N2 - 79 79 -
3 C 21+.05N4 - - .05N4
4 CaO - - - .94N4
5 CaCO3 .95N4 - - .01N4
6 CO2 - - 21+.94N4 -
Rate of reactions: 1) .94N4 the rate of production of CaO
2) 21 to consume all entering O2
Before we solve it, we must write a short
function to iterate with ssec2 (calling
N4: x as the single unknown):
function err=exr828(x)
%
% this function solves problem 8.28 in Reklaitis using reacten,
% when iterated with ssec2
%
setne('s',1,25,[.05*x+21 .95*x],[3 5])
err=reacten('vs',[315.6 950],1:2,3:4,[.94*x 21],[1 1 0 0 0 1]);
Notes:
a) in the first line the flows of C and CaCO3 are set
as shown in the table.
b) in the second line the reactions are carried out after streams 1
& 2 are mixed and followed by a separation of the product into
the vapor stream (3) at 600C with N2 and CO2 in
it and the solid stream (4) at 950C.
Then we can solve the problem after using start301 by:
Here are your compounds' formulae and names:
No. Formula Name
----------------------------------------
1 O2 oxygen
2 N2 nitrogen
3 C carbon
4 CaO calcium oxide
5 CaCO3 calcium carbonate
6 CO2 carbon dioxide
Here are your reactions:
----------------------------------------
1) CaCO3 --> CaO + CO2
2) O2 + C --> CO2
Enter the number of streams: 4
>> Tdeg='C';
>> setne('v',2,25,[21 79],1:2) <-- set the feed
>> exr828(25)
ans =
-1.5920e+03
>> exr828(35) <-- There must be a root in the interval 25->35
ans =
702.0396
>> ssec2([25 35],'exr828(x)')
ans =
31.9398
>> exr828(ans)
ans =
0
>> showe(1:2,3:4,10,2)
Inlet | Outlet
Stream 1 2 Total | 3 4 Total
Tmp C 25.00 25.00 | 315.56 950.00
State solid vapor | vapor solid
Entlpy -36620.68 0.00 -36620.68 |-18770.19 -17850.49 -36620.68
Compound Stream Flows
oxygen 0.00 21.00 21.00 | 0.00 0.00 0.00
nitrogen 0.00 79.00 79.00 | 79.00 0.00 79.00
carbon 22.60 0.00 22.60 | 0.00 1.60 1.60
calcium oxide 0.00 0.00 0.00 | 0.00 30.02 30.02
calcium carbonate 30.34 0.00 30.34 | 0.00 0.32 0.32
carbon dioxide 0.00 0.00 0.00 | 51.02 0.00 51.02
Total 52.94 100.00 152.94 | 130.02 31.94 161.96
>> 30.34/22.60
ans =
1.3425
Thus the ratio we need is about 1.34 moles CaCO3 for every
mole of C.