[Go to previous section: 3.1| Go to next section: 3.3]
[ Go to CENG301 Homepage | CENG301 Notes Table of Contents]

3.2: Conservation of Energy: Terms in an Energy Balance

• 3.2.1 Energy Balance for a Closed System
• 3.2.2 Balance for an Open Steady State System

There are three terms that may be important in determining the total energy in a system:

a) Potential energy
b) Kinetic energy
c) Internal energy

For a system that is a single object with mass m, these terms are:

a) E_P = mgh
b) E_K = .5mv2
c) E_U = m

where:

g =	the gravitational field constant,
h =	the height above a datum plane of the center of the object perpendicular to the direction gravity acts,
v =	the velocity of the object relative to some "fixed" object,
=	the internal energy per unit mass of the object.

This assumes that gravity is the only field acting on the object. In essence, the internal energy term accounts for all forms of energy except potential and kinetic. The internal term includes the effect of:

1. the state of the matter in the object; i.e. whether it is a gas, liquid or solid, or some mixture of these;
   
2. temperature variations from some reference temperature;
   
3. pressure variations from a reference pressure;
   
4. the composition of the object.
   

Note particularly that each term in this classification is measured relative to some state or position that is considered to be the zero point for calculating energy.

The sum of these three forms of energy is the total energy of the object. Thus we define:

The total energy of an object may change as a result of heat transferred to (or from) it, or by it doing work on the surroundings (or the surroundings doing work on it). If those are the only ways that the object's energy can change, we say that it forms a closed system. Thus its boundaries are impervious to the flow of mass in both directions. A system that is open has porous boundaries so that mass can flow across them. In an open system, we must account for the energy added to (or taken from) it by this mass flow across its boundaries.

3.2.1 Energy Balance for a Closed System

First, we will give the general energy balance for a closed system expressed in terms of the change that occurs over a finite time interval:

where:

ET(t) =	the total energy of the object at time t,
Q =	the heat added to the object from time t1 to t2 and
W =	the work done by the object from time t1 to t2.

The differential form for this is:

where:

q =	the rate of heat addition to our system and
w =	the rate our system does work on the surroundings.

The most common forms of work encountered in chemical systems are:

a) work associated with motion acting against friction as in stirring a liquid and
b) work associated with expansion of fluids.

The work done by an object in expanding from volume V₁ to V₂ against an external pressure p is:

The energy carried into a system across its boundaries may be categorized in the same three forms as the energy of the system itself. If the rate of flow into the system is F mass/time then the rate of addition of energy is:

F(.5v² + gh + )

In this expression the velocity, height and internal energy per mass all must be evaluated at the conditions where the mass flows across the boundary. This motion also has a work term associated with it. The rate at which work must be done by the surroundings to get the mass into the system is:

Fp

where:

=	the specific volume of the fluid
p =	the pressure

Thus the sum of the rate of addition of energy carried in and the work done in getting it in is:

F(.5v² + gh + + p )

The last two terms in this expression are usually combined as:

+ p =
where is the enthalpy per mass of fluid.

If we have a product stream that flows out of the system at a rate F^out, it carries energy with it and the system must be doing work to get it out. That looks the same as for a feed:

Energy lost + Work done = F^out(.5(v^out)² + gh^out + ^out)

where we have put the superscript out on terms to indicate that they must be evaluated at exit conditions.

3.2.2 Balance for an Open Steady State System

All of the open systems that we encounter in this course are steady state systems in which the total energy of the system is constant. Then for such a system (since dE_T/dt = 0) our energy balance looks like:

0 = q - w' + Fⁱⁿ(.5(vⁱⁿ)² + ghⁱⁿ + ⁱⁿ) - F^out(.5(v^out)² + gh^out + ^out)

where w' is the rate of work the system is doing excluding the
work associated with the flows in and out of the system.

Flows in the feed and product streams at steady state system must be equal since mass is conserved:

so we could combine the terms inside the two sets of brackets. In a more general system with several inlet and exit streams there is no particular advantage to be taken of this property. For our general steady state system our balance equation expressed in mass units is:

where:

j	designates the jth stream in or out of the system and
Fj	is positive for feed streams and negative for product streams.

If we wish to calculate the energy in our streams in terms of molar rates, our balance will look like:

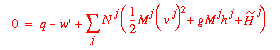
where:

Nj =	the molar flow rate in stream j (positive for a feed and negative for a product stream)
=	the molar specific enthalpy of a fluid.
Mj =	the average molecular weight of stream j.

In most chemical systems like reactors and separators the kinetic and potential energy components in the balance are unimportant so that the balance reduces to:

If we insist on flow rates that are positive, we can split our sum in this equation into two parts:

The calculation of the molar specific enthalpy of a fluid is considered in the section of these notes on energy balances.