[ Go to CENG301 Homepage | CENG301 Notes Table of Contents]
Skip to 3.4.2 Degree of Freedom Table for Energy Balances
[Go to previous section: 3.3]
[ Go to CENG301 Homepage |
CENG301 Notes Table of Contents]
![]()
Skip to 3.4.2 Degree of Freedom Table for Energy
Balances
Problem: Determine the heat that must be added to a reactor in which CO2 and H2 react to produce methane and water by:
The inlet stream contains 1 mol CO2, 3 mols H2 and 0.5 mols N2 and is at 500K and 1 atm. The exit stream contains 0.5 mols of H2 and is at 600K and 1 atm.
We will assume that the specific enthalpy of each compound depends
only on the compound and the temperature since the pressure is fixed
and all streams are gaseous. We will designate the specific enthalpy
of compound A at temperature T by ![]() A(T).
The reaction rate must be 2.5/4 or 0.625 so the flow rates and
specific enthalpies of the two streams look like:
A(T).
The reaction rate must be 2.5/4 or 0.625 so the flow rates and
specific enthalpies of the two streams look like:
Inlet Exit Compound Flow Enthalpy Flow Enthalpy 1 CO2 1.0001(500) 0.375
1(600) 2 H2 3.000
2(500) 0.500
2(600) 3 N2 0.500
3(500) 0.500
3(600) 4 CH4 0.000
4(500) 0.625
4(600) 5 H2O 0.000
5(500) 1.250
5(600)
Two different methods will be used to find Q. Both are based on:
|
1) |
|
The heat of reaction with all reactants and products as ideal
gases depends only on the temperature and is:
Then we may find Q as:
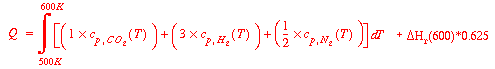
The problem then is to determine the heat of reaction at 600K. To do
so we need to use the heats of formation for each of the reactants
and products in the reaction defined by:
![]()
where the formula for A is:
(E1)e1(E2)e2
.........
and Ej is the jth element
Normally the pressure, P, and the state, s, in the specific enthalpy of A are taken to be 1 atm and the state that the compound would normally be found in at 25°C (298K) and 1 atm. This is then designated as the "standard" heat of formation of A. The heats of formation in the Appendix in Reklaitis are for all compounds as ideal gases regardless of their normal states at 25°C and 1 atm. This makes it particularly simple to determine the heat of reaction for all gas reactants and products by writing for our specific reaction:
|
|
|||
|
|
- |
+ |
|
|
+ 2( |
- |
+ |
|
|
- ( |
- |
+ |
|
|
- 4( |
- |
+ |
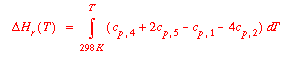
|
+ |
- |
+ |
|
|
+ 2( |
- |
+ |
|
|
- ( |
- |
+ |
|
|
- 4 |
Note that the enthalpies of the elements at 298K cancel out in
this relation since the equation is balanced. Thus we are left
with:
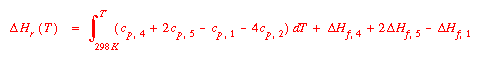
This same procedure extends to the determination of the heat of
any reaction, but we must be careful to account for phase changes if
either:
a) the heats of formation are "standard" or
b) the compounds in the reaction are not gaseous.
An alternate procedure that gives the same results starts with the
same original expression for Q and determines the specific enthalpies
directly:
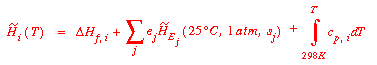
In any steady state system the molar flow rates of the elements
into and out of the system must be equal. Thus the specific
enthalpies of the elements can not appear in the final result for Q.
An equivalent way to calculate Q is to determine the specific
enthalpies of all compounds with the enthalpies of the elements taken
as 0. This leaves us with:
|
2) |
|
|
3) |
|
a) Calculate the enthalpy for all species relative to the elements by either 2) or 3) depending on the state of the stream that it is in.
b) Determine Q from 1) using these specific enthalpies.
We can see how the two procedures work with the programs discussed in
the last section of these notes. First we will actually find the heat
of reaction at 600K and then add to it the amount of heat required to
heat the inlet gases to 600K. In any case we need the names of our
compounds so we use start301:
Input the name of your new file: sab Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 CO2 carbon dioxide 2 H2 hydrogen 3 N2 nitrogen 4 CH4 methane 5 H2O water Here are your reactions: ---------------------------------------- 1) CO2 + 4H2 --> CH4 + 2H2O Enter the number of streams: 4
Now let's follow the heat of reaction approach.
In this problem all compounds are vapors, so we need the heat
capacity polynomials for the vapors:
cpv = 19.0200 0.0796 -0.0001 0.0000 -0.0000 17.6300 0.0670 -0.0001 0.0000 -0.0000 29.4100 -0.0030 0.0000 0.0000 -0.0000 38.3800 -0.0737 0.0003 -0.0000 0.0000 34.0400 -0.0097 0.0000 -0.0000 0.0000
Our only reaction:
has already been defined.
>> stoic
stoic =
-1 -4 0 1 2
The heat of formation for all compounds is stored in:
>> StdhkJ' <-- Note StdhkJ is stored as a column vector ans = -393.5000 0 0 -74.8500 -241.8300
The heat of reaction at 298.15K is then:
>> dhr298=stoic*StdhkJ dhr298 = -165.0100
The difference in heat capacity coefficients for a stoichiometric
amount of product compared to that of the reactant is found by:
>> cpt=stoic*cpv cpt = 16.9200 -0.4406 0.0010 -0.0000 0.0000 >> format long >> cpt cpt = Columns 1 through 4 16.92000000000001 -0.44058000000000 0.00095618000000 -0.00000076533000 Column 5 0.00000000021320
We may use this to find the heat of the reaction at 600K:
>> format short >> dhr600=dhr298+.001*enth1(298.15,600,cpt) dhr600 = -179.2968
The heat capacity of the feed (per mol of CO2) has the
coefficients:
>> format long >> cpin=[1 3 .5 0 0]*cpv cpin = Columns 1 through 4 86.61499999999999 0.27911500000000 -0.00046517500000 0.00000035741550 Column 5 -0.00000000009756
We may use this to calculate the heat that must be added per mol of
CO2 fed:
>> q=(.625*dhr600)+.001*enth1(500,600,cpin) q = -97.06983363470445
Use start301 as with the first approach, then set
the feed stream with setne:
>> setne('v',1,500,[1 3 .5],1:3)
Then react this stream to form a product at 600K with fraction
0.625 of the CO2 converted:
>> reacte('v',600,1,2,.625)
ans =
-97.06983363470442
Our answer has the same value we found by the heat of reaction
approach. We can also display our results:
>> showe(1,2,10,3)
Inlet | Outlet
Stream 1 | 2
Tmp K 500.00 | 600.00
State vapor | vapor
Entlpy -364.5 | -461.6
Compound Stream Flows
CO2 1.000 | 0.375
H2 3.000 | 0.500
N2 0.500 | 0.500
CH4 0.000 | 0.625
H2O 0.000 | 1.250
Total 4.500 | 3.250
The equilibrium constant, K, for a equilibrium reaction is a function
of the standard Gibb's free energy change for the reaction,
![]() G°,
and temperature T:
G°,
and temperature T:
The standard state Gibb's free energies of formation for reactants
and products are normally given at a temperature of 298.15 K and 1
atm. The Gibb's free energies of formation for compounds at 25°C
and 1 atm is in the Appendix of the notes. ![]() G°(298.15K)
is calculated in the same manner that
G°(298.15K)
is calculated in the same manner that ![]() H°(298.15K)
is calculated from enthalpies of heats of formation. The equilibrium
constant at 298.15K for a reaction can be easily calculated from the
data for
H°(298.15K)
is calculated from enthalpies of heats of formation. The equilibrium
constant at 298.15K for a reaction can be easily calculated from the
data for ![]() Gf°.
Gf°.
In order to calculate K at another temperature, an expression for
![]() G°
as a function of temperature is needed.
G°
as a function of temperature is needed. ![]() G
is related to the change in enthalpy
G
is related to the change in enthalpy ![]() H,
and change in the entropy,
H,
and change in the entropy, ![]() S,
by:
S,
by:
If the derivative of ![]() G°/RT
is taken with respect to T at constant entropy, and the expression
for K is used, then the following relationship is obtained:
G°/RT
is taken with respect to T at constant entropy, and the expression
for K is used, then the following relationship is obtained:
Consequently, the enthalpy as a function of temperature must be
known, which we have shown previously:
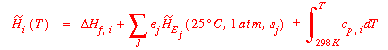
When the above equation is integrated for ![]() H°,
the references to the elements are eliminated. If the Sabatier
reaction was the equilibrium reaction, the integrated relationship
would be:
H°,
the references to the elements are eliminated. If the Sabatier
reaction was the equilibrium reaction, the integrated relationship
would be:
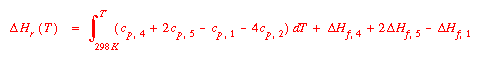
Remember that each Cp is a function of temperature. Substitution of
this relationship into the expression for the derivative of ln K,
then another integration will yield a relationship of the form:
where J is the integration constant from the relationship for
![]() Hr(T)
and I is the integration constant for the last integration. The
integration constants are determined by evaluation of each of the
last two relationships at 298.15K. J can be determined uniquely form
the expression for
Hr(T)
and I is the integration constant for the last integration. The
integration constants are determined by evaluation of each of the
last two relationships at 298.15K. J can be determined uniquely form
the expression for ![]() Hr(T)
and I from the expression for ln K. Since
Hr(T)
and I from the expression for ln K. Since ![]() G°
= - RT ln K, I can be evaluated at 298.15K using Gibb's free energies
at the standard state at 298.15K. Once the integration constants are
known, then the expression for ln K can be evaluated for any
temperature.
G°
= - RT ln K, I can be evaluated at 298.15K using Gibb's free energies
at the standard state at 298.15K. Once the integration constants are
known, then the expression for ln K can be evaluated for any
temperature.
The function kequil will
calculate equilibrium constants for gas phase reactions at any
temperature as long as the reactions are set in stoic. Help
on kequil gives:
>> help kequil
kequil - sets the equilibrium reactions for gas phase reactions
function keq=kequil(t2,j)
Argument list
Argument Gives
t2 temperature in units of Tdeg
j indices of the reactions that will be at equilibrium
Function return the variable: keq,
for reactions specified and will put a zero for reactions in
which equil. const. is _not_ solved for. If j is omitted,
equil. constant for all reactions in stoic will be determined.
Example : keq1=kequil(550,[1 3])
LDM
Here we will use kequil to solve example
15.5 in Smith and Van Ness (page 510) : Calculate the
equilibrium constant for the vapor-phase hydration of ethylene at 145
and 320 C. The reaction is C2H4(g) +
H2O(g) ---> C2H5OH(g).
After start301:
Input the name of your new file: eths Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 C2H4 ethylene 2 H2O water 3 C2H5OH ethanol Here are your reactions: ---------------------------------------- 1) C2H4 + H2O --> C2H5OH Enter the number of streams: 2 >> kequil(418.1) ans = 0.1154 <--- value in Smith and VanNess, K = .1426 >> kequil(593.15) ans = 0.0022 <--- value in Smith and VanNess, K = .00291
The equilibrium constant K is related to the mol fractions at
equilibrium and if a gas, pressure. For gases, this is:
For liquids, this is:
The mol fractions can be related to reaction
rates and initial molar flows. The function reactee
is a reactor module for a single equilibrium reaction. Help on
reactee gives:
>> help reactee
reactee: energy-balance equilibrium reactor module
function er = reactee(s,tmp,in,out,rsx,jv,P)
Argument List:
Argument Gives
s the state of the exit stream: 'v'
tmp the temperature of the exit stream in Tdeg.
in the index(ices) of the inlet streams.
out the index of the exit stream.
rsx guess for reaction rates
jv indices of reactions that will be at equilibrium
P pressure of the exit stream
reactee returns the error between the keq(thermo)
and the product of partial pressures from kvalp.m
Ex. cs = ssec2([0 .95],'reactee(''v'',1393,1,2,x,1,1)')
would give the equilibrium extent of reaction in vapor
stream 2 with temperature 1393Tdeg and 1(unit pressure)
for reaction 1 and inlet stream 1
LDM
Now we will solve example 15.8 in Smith and Van Ness (page 521) using the modules: In a laboratory investigation, acetylene is catalytically hydrogenated to ethylene at 1120 C and 1 bar. If the feed is an equimolar ratio of acetylene and hydrogen, what is the composition? The reaction is C2H2(g) + H2(g) --> C2H4(g). After using start301.
Input the name of your new file: acet
Here are your compounds' formulae and names:
No. Formula Name
----------------------------------------
1 C2H2 acetylene
2 H2 hydrogen
3 C2H4 ethylene
Here are your reactions:
----------------------------------------
1) C2H2 + H2 --> C2H4
Enter the number of streams: 2
>> setne('v',1,1393,[1 1 0])
>> kequil(1393)
ans =
1.0725 <-- value in Smith and VanNess is ~1
for this reaction at 1393 K
>> cs = ssec2([0 .95],'reactee(''v'',1393,1,2,x,1,1)'
cs =
0.3054 <---- value in Smith and VanNess is 0.2929
>> showe(1,2,10,3)
Inlet Outlet
Stream 1 2
Tmp K 1393.00 1393.00
State vapor vapor
Entlpy 327.7 274.4
Compound Stream Flows Equil. comp. Reference value
acetylene 1.000 0.695 0.4097 0.4142
hydrogen 1.000 0.695 0.4097 0.4142
ethylene 0.000 0.305 0.1806 0.1716
Total 2.000 1.695
>> kvalp(1,2,1)
ans =
1.0708 <--- very close to 1
The degree of freedom table for energy balances is very similar to
the one for material balances. Only a few new variables such as
dW/dT, dQ/dT, and the stream temperatures have to be considered. In
addition, one also has to consider the addition of the energy balance
equation. Finally, the new degree of freedom table will just combine
material and energy balances.
A process gas stream at 400°C is to be considered rapidly cooled
to 200°C by direct quenching with cold liquid benzene at
200°C. The hot stream consists of 40%
C6H6, 30%
C6H5CH3, 10% CH4, and 20%
H2. The gas feed rate is 1000 kgmol/hr.
|
Unknowns |
||||
|---|---|---|---|---|
|
|
Material Balance Sub problem |
Combined Balance Problem |
||
|
Type |
Number |
From |
Number |
From |
|
Stream Vars. |
9 |
4 each in Streams 2&3 |
9 |
4 each in Streams 2&3 |
|
Temperatures |
|
|
3 |
1 in each Stream |
|
dQ/dT,dW/dT |
|
|
2 |
Always two |
|
Total |
9 |
|
14 |
|
|
Balances and Specifications |
||||
|
|
Material Balance Sub problem |
Combined Balance Problem |
||
|
Type |
Number |
From |
Number |
From |
|
Material Bal. |
4 |
4 Species |
4 |
4 Species |
|
Energy Bal. |
|
|
1 |
See below |
|
Compositions |
3 |
4 Comps are given in |
3 |
4 Comps in Stream |
|
Temperatures |
|
|
3 |
All 3 Temps. |
|
dQ/dT,dW/dT |
|
|
2 |
Both = 0 |
|
Basis |
1 |
given 1000 kgmol/hr |
1 |
1000 kgmol/hr |
|
Total |
8 |
|
14 |
|
|
|
Material Balance Sub problem |
Combined Balance Problem |
||
|
Degree of Freedom |
1 |
|
0 |
|