(Click on images to enlarge)

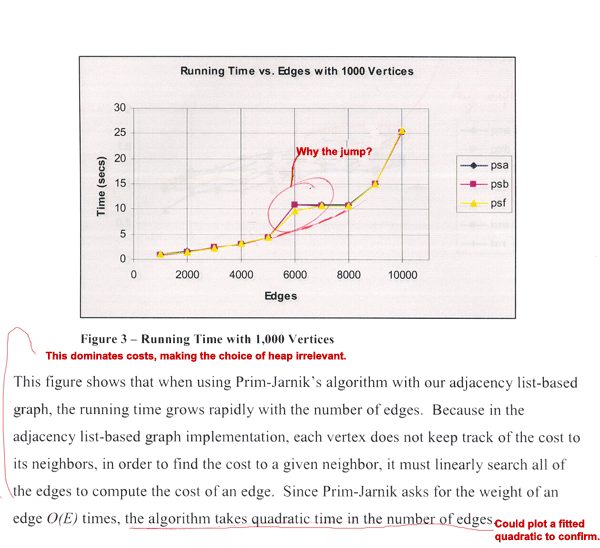
In the above samples, the students fail to explain key features of the data they produced. In Sample 1, the plot lines jump at 6000 edges from a nice curve that reflects the expected theoretical asymptotic behavior. Explaining this jump should be part of the analysis. Potential causes to explore include:

• Atypical test data at 6000 (and 7000) edges. To reduce the effects of atypical data, you typically want to average over several test data of each size.
• Memory hierarchy effects at this particular data size. You should be familiar with the details of your platform's memory hierarchy to be able to explore such issues.
• Stair-step data structure that isn’t captured by the chosen data sizes. Test for this by adding more data points.
• Data density issues. Edge density is this case is increasing while the number of vertices is held constant. At 6000 edges, the graph may be sufficiently dense for the algorithm to be significantly slower.
• System load. Your timings should not include CPU time spent on other tasks, and you should limit what other system resources are needed during testing. This is unlikely to be the cause here since the behavior is consistent across algorithms.

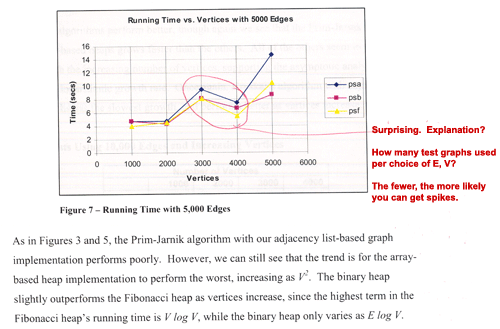
In addition to failing to explain the data anomaly in Sample 1, the authors fail to explain the spike at 3000 vertices in Sample 2, which is even more anomalous since it is slower at 3000 vertices than at 4000 vertices.

Finally, the authors claim that the plot lines in Sample 1 conform to the theoretical quadratic asymptote. While that looks plausible, the claim could be confirmed by fitting and plotting a quadratic curve.

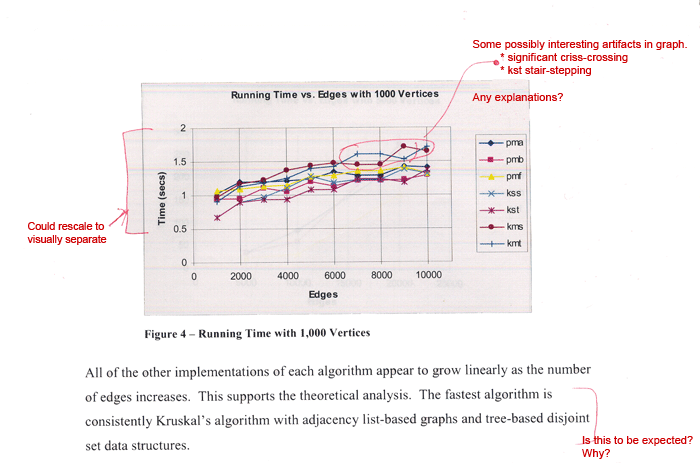
This sample has some artifacts that could be interesting, but are not explained.

• The lines criss-cross in several places. Because the lines are always close together (i.e., within a small percentage of each other), the authors might validly consider the crossing behavior to indicate insignificant noise. If so, the argument should be made and referenced to the margin of error of your timing mechanism. Also, was the same data used for each algorithm? It should be, for consistency.
• The data exhibits significant stair-stepping. This is typically a result of either the algorithm or memory hierarchy issues.
  
  

Explanation of issues and suggested improvements for Sample 4

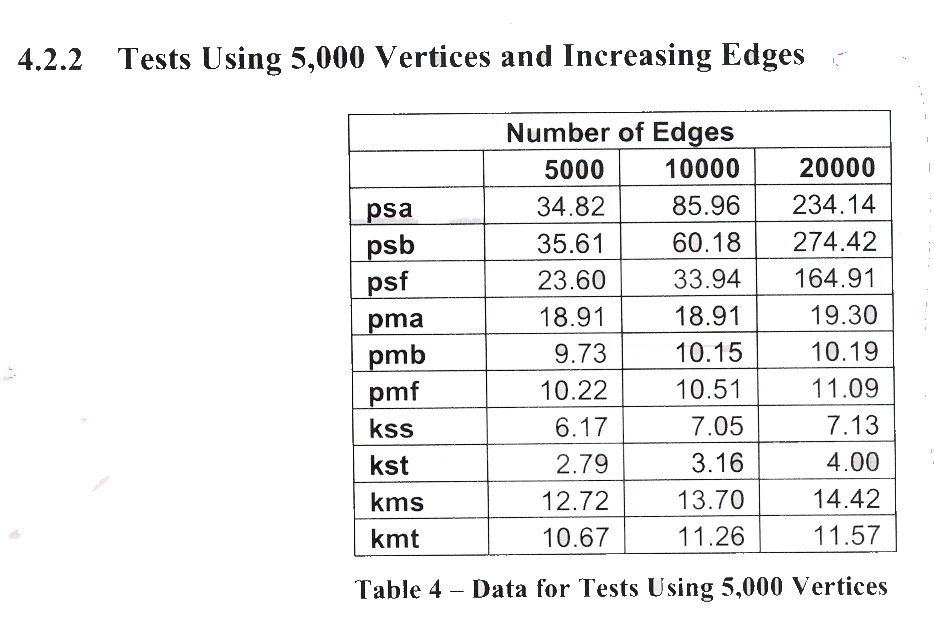
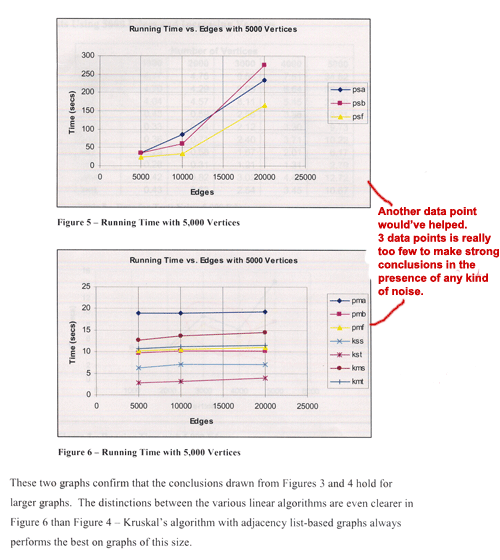
The table and associated figures shown above have two problems.

• Only three data sizes are used, an insufficient number to draw strong conclusions about trends
• While the authors correctly state that the data confirms the expected conclusions, they should be more explicit and say, for example, that this illustrates that pmb is consistently faster than pmf, which is consistently faster than pma, as expected from the algorithms' descriptions. However, it is somewhat surprising that kmt isn't consistently faster than kms. The paucity of data, however, makes it hard to say how consistent this behavior is.