Zerotree data structure

A wavelet coefficient x is said to be insignificant with respect to a given threshold T if |x|<T. The zerotree is based on the hypothesis that if a wavelet coefficient at a coarse scale is insignificant with respect to a threshold, then all wavelet coefficients of the same orientation in the same spatial location at the finer scale are likely to be insignificant with respect to the same threshold. More specifically, in a hierarchical subband system, with the exception of the highest frequency subbands, ever coefficient at a given scale can be related to a set of coefficients at the next finer scale of similar orientation. The coefficient at the coarse scale is called the parent, and all coefficients corresponding to the same spatial location at the next finer scale of similar orientation are called children. Similar, we can define the concepts descendants and ancestors.The data structure of the zerotree can be visualized in Figure . Given a threshold T to determine whether or not a coefficient is significant, a coefficient x is said to be an element of a zerotree for the threshold T if itself and all of its descendents are insignificant with respect to the threshold T. Therefore, given a threshold, any wavelet coefficient could be represented in one of the four data types: zerotree root (ZRT), isolated zero (IZ) (it is insignificant but its descendant is not), positive significant (POS) and negative significant (NEG).

  

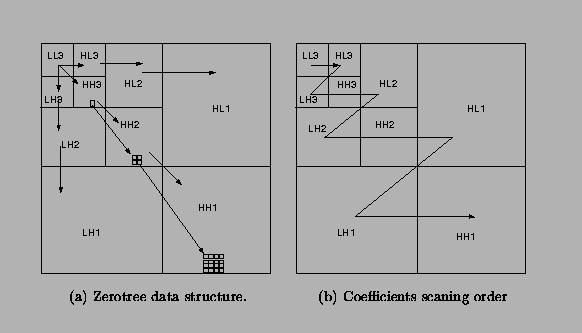Figure: Coefficients are coded in a zerotree structure and scanned in a left-to-right order.