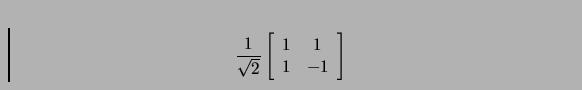
The Haar Wavelet Transform performs sum and difference calculations on the input image data. The actual transform is as follows:
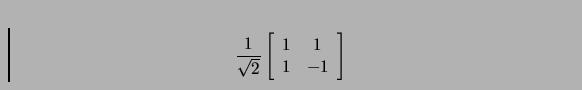
This transform can be applied to adjacent horizontal points (paired off in twos), then adjacent vertical cells. The transform is then run again on the upper left quadrant of the new image. The process can be repeated until you get down to a two-by-two image in the upper left quadrant, although it turns out that a minimum block size of 16-by-16 or 32-by-32 is ideal for compression. The new image is the same size as the previous image, but most of the information is located in the upper left smallest block. This block contains the normalized average of the original image, scaled to a smaller block size. The rest of the image contains a mix of the addition and subtraction information. The idea is that most of the adjacent pixels of the original picture have close to the same value as each other, so storing the difference between them requires a small number of bits. The actual bit allocation algorithm will be discussed in the next section.
Once we have assigned the number of bits we want to represent each pixel, we can use the same transform to invert our data and return to the original image. Note that the Haar wavelet transform is equal to its inverse. You can view an example of a transformed image in the ``Sample Images'' section of the web page.