The DCT is fast to calculate and is optimal for images that are highly
correlated. Unlike the Fourier Transform, the DCT is all real, which
means that for an
image, we will also have
coefficients. Like
the
Fourier Transform, the DCT provides a 1-to-1 mapping. Therefore,
to get
back the original image, we simply take the IDCT of
the our transformed
image. We can find the DCT by using the following formula:
and C(u) = 1 for
.
DCT images typically look like the following:
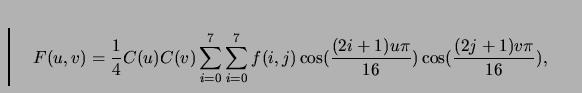
The bright regions correspond to big coefficients and the black regions correspond to small coefficients. If we then divide the image into a number of small blocks, we can allocate bits for each block, where the blocks on the top left corner would be encoded with many bits, and the ones at the bottom right corner would be coded with few or no bits. The allocation of encoding bits is distributed by means of a mask. We divide the DCT into 16x16 blocks and all the coefficients of the block is encoded with the same number of bits.
