The Grashof number is a dimensionless quantity used in analyzing the velocity distribution in free convection systems. In the systems encountered most commonly in BSL, free convection is is the natural tendency of a substance to migrate due to some driving force. In free convection, the driving force is a buoyancy force caused by a temperature gradient, as the fluid would be at rest in the absence of temperature variations. The Grashof number is analogous to the Reynolds number in forced convection.
Essentially, the Grashof number is a ratio of buoyant forces to viscous forces.
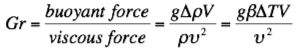
When Gr >> 1, the viscous force is negligible compared to the buoyancy and inertial forces. When buoyant forces overcome the viscous forces, the flow starts a transition to the turbulent regime. For a flat plate in vertical orientation, this transition occurs around Gr = 10e+9.
In terms of viscosity, the Grashof number can be defined defined as in the following 2 ways:
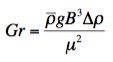
where:
Δρ = total change in density between regions of high temperature and low temperature
This can be obtained by expanding ρ in a Taylor series about the mean temperature.
The most useful form for Matlab application is:
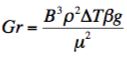
where:
β = the inverse of the film (mean) temperature
ρ = the density evaluated at the mean temperature
g = the gravitational constant
ΔT = the temperature difference
B = the distance between regions of high temperature and low temperature
μ = the viscosity of the convecting fluid
For this project, a MATLAB program has been developed that links to the 301 database and can be used to calculate the Grashof number. Quick link to the code itself: grcalc.m
Because the Grashof number is the characteristic dimensionless group of free convection, it arises in problems dealing with heat transfer coefficient correlations.
Examples:
See BSL Example 14.6
See SK,KY Example 10.1
Home
