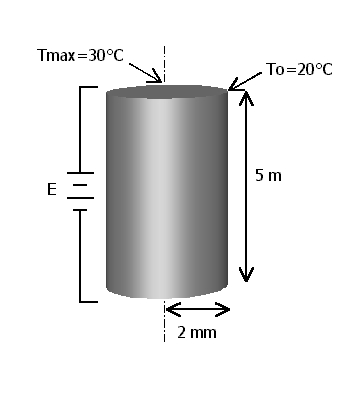
Problem: A copper wire has a radius of 2 mm and a length of 5 m. For what voltage drop would the temperature rise at the wire axis be 10°C, if the surface temperature of the wire is 20°C?

To see the Maple solution for the shell balance differential equation, click here.

Solution:

Start with equations 9.2-1 and 9.2-14 (obtained from solution of shell balance differential equation to get equation 9.2-17

> restart;I^2; We don't want to use I for the current

> Se:=i^2/ke; eq 9.2-1 but using i for the current density instead of I since Maple thinks I is sqrt(-1)

> dTmax:=Se*R^2/(4*k); eq 9.2-14 now leads to eq. 9.2-17

> i:=ke*E/L; eq. 9.2-18

> dTmax; giving eq. 9.2-19

> eq19:=dTmax=Tmax-T0; dTmax is the temperature difference between the wire axis and the wire surface.

> s:=solve(eq19,E); Now we solve the above equation for E, the voltage drop.

> E:=s[1]; Giving us eq 9.2-20. The voltage drop is positive, so we want the positive root, which is s[1], the first element of s.

> R:=2*mm; L:=5*m;T0:=293*K; Tmax:=T0+10*K; Given data with units

> k:=2.23e-8*volt^2*K^(-2)*ke*T0; We are also given the value for the Lorenz number of copper

> E; Close to eq. 9.2-21 except:

> mm:=m/1000; We need the relation between m and mm.

> E; And we need to tell Maple that ke and volt are positive real variables.

> assume(ke>0);assume(volt>0);

> simplify(E);