[ Go to CENG301 Homepage | CENG301 Notes Table of Contents]
[Go to previous section: 1.4| Go
to next section: 1.6]
[ Go to CENG301 Homepage
| CENG301 Notes Table of Contents]
![]()
Page 1
The modules illustrated in previous sections were idealized
systems that are rarely encountered in a chemical plant. Few chemical
units perform a single function. Even fewer units have data for them
posed in such a way that you can directly solve for all flow rates in
the streams that lead in and out of them without:
a) solving simultaneous linear equations or
b) solving one or more nonlinear equations.
We will look at examples of both problems in this section. A
distillation column with known feed stream, but composition
specifications on the product streams is frequently encountered. The
function fraco (for FRACtions Out) was written to
solve for the fraction of each compound in the feed that is sent to
the top for such specifications. This then allows us to use the
sep function to complete the analysis. The problem
as posed requires only that we solve simultaneous linear equations: a
job that MATLAB does very efficiently.
Next we will consider typical specifications on the performance of a
reactor in which two competing reactions occur. Again we will find
that for common specifications this leads to the solution of
simultaneous linear equations.
As with the mass flow modules, extra help and diagrams can be
accessed by simply adding the prefix picto the module
name.
Finally we will conclude with illustrations that require the use of a
trial and error routine to handle nonlinear terms. We will restrict
this to the case where we can pose the problem as a single nonlinear
equation in one unknown. In later sections of the notes we will look
at some ways to extend this to more general nonlinear problems.
Help applied to the function fraco tells us a lot
about the way the function works.
>> help fraco
frac=fraco(lk,xdhk,xblk,in)
Auxiliary function that gives the fraction of compounds sent to the
distillate in fractions
Argument Gives
lk index of light key
xdhk mol fraction of heavy key in distillate
xblk mol fraction of light key in bottom
in index of the feed stream in ns
Heavy key must be next to the light key
For additional help and picture, see PICFRACO
Example: >> ti=fraco(2,0.03,0.05,3);
>> sep(ti,3,[2 4])
OKB, TYLC
Here is the image of fraco.
The nomenclature adopted in describing the operation of
fraco is commonly used in the separations
literature. We would like to get an approximate analysis of a
distillation unit used to separate a multicomponent mixture. We
assume the compounds will behave "normally" in the sense that we can
order them such that each compound will be more enriched in the top
product than all compounds that follow it. We will then list our
compounds in such a order (called in decreasing "volatility"). Then
we focus on two key compounds called the light and heavy keys. The
job of the separator is to make the mol fraction of the light key in
the bottom product meet a given specification and the mol fraction of
the heavy key in the top product meet another specification. If the
separator is a distillation unit and the compounds are ones
frequently encountered in the petroleum industry, then we find:
1) essentially all of the compounds lighter than the light key are
removed from the bottom product,
2) essentially all of the compounds heavier than the heavy key are
removed from the top product.
The situation in which the two keys are next to one another in our
ordered list can then be solved for a given feed. To do so pick as a
basis one mol of feed with mol fractions: z1,
z2, ...zH. Then list the molar flow rates for
all compounds in the feed and product streams and use the two
assumptions given above:
|
Compounds |
Feed |
Distillate |
Bottom |
|---|---|---|---|
|
1 |
N1=z1 |
ND1 = z1 |
NB1 = 0 |
|
2 |
N2=z2 |
ND2 = z2 |
NB2 = 0 |
|
............................................................ .. |
|||
|
LK |
NLK=zLK |
NDLK |
NBLK |
|
HK |
NHK=zHK |
NDHK |
NBHK |
|
............................................................ .. |
|||
|
H |
NH=zH |
NDH = 0 |
NBH = zH |
|
_________ |
_________ |
_________ |
|
|
Total |
1 |
D |
B |
Mass balances for the keys require that:
Thus there are only two unknowns to solve for: e and m.
Fortunately we have the two specifications:
to determine our unknowns. We can also find B and D in terms of
the two unknowns:
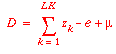 and
B = 1 - D
and
B = 1 - DIf we multiply out the equations that determine the unknowns, they
form two linear equations.
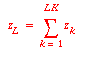
Fraco performs this analysis and uses the
solutions of the equations to find the fraction of each compound that
goes to the distillate stream.
We can use fraco to solve for the flows in the
streams attached to a distillation unit separating the same compounds
used to illustrate sep in the last section of the
notes. Suppose we have the same feed and pick the two butanes as our
key compounds. We have the following specifications for the keys:
xBLK = 0.05
<-- mol frac i-Butane in the Bottom
xDHK = 0.03
<-- mol frac n-Butane in the Top
After using start301, (3) Other, to set our
names:
You have chosen to not use any compound data
If you wish to enter data for a compound, exit (control-C)
then execute "create", then run a "new session", choice (1)
Enter the number of compounds: 4
Compound names must be less than 25 characters long!
Give the name of compound # 1: propane
Compound names must be less than 25 characters long!
Give the name of compound # 2: i-butane
Compound names must be less than 25 characters long!
Give the name of compound # 3: n-butane
Compound names must be less than 25 characters long!
Give the name of compound # 4: i-pentane
How many streams will there be?5 <----this line sets up the initial
flow matrix with all zeros
>> ns(3,:)=[20 30 30 20]; <-- This inserts the feed flows
Then use fraco, sep and
showm to see our results:
>> ti=fraco(2,.03,.05,3)
ti =
1.0000 0.9149 0.0489 0
>> sep(ti,3,[2 4])
>> showm(3,[2 4],10,4)
Compound Inlet | Outlet
Stream 3 | 2 4 Total
propane 20.0000 | 20.0000 0.0000 20.0000
i-butane 30.0000 | 27.4457 2.5543 30.0000
n-butane 30.0000 | 1.4674 28.5326 30.0000
i-pentane 20.0000 | 0.0000 20.0000 20.0000
Total 100.0000 | 48.9130 51.0870 100.0000
Now check to see that the specifications were met:
>> 1.4674/48.9130
ans =
0.0300
>> 2.5543/51.0870
ans =
0.0500
There is always the possibility that we may divide by zero if there
are some compounds with zero flow rates in the feed stream. This does
not bother us too much in MATLAB and only leads to warnings. A slight
modification of the last example with zero flow of a fifth compound
is shown next.
>> cnms=['C3 ';'I-C4';'N-C4';'I-C5';'N-C5'];
>> ns=zeros(3,5);
>> ns(1,:)=[20 30 30 20 0];
>> ti=fraco(2,.03,.05,1)
Warning: Divide by zero
ti =
1.0000 0.9149 0.0489 0 0
>> sep(ti,1,[2 3])
>> showm(1,[2 3],10,4)
Compound Inlet | Outlet
Stream 1 | 2 3 Total
C3 20.0000 | 20.0000 0.0000 20.0000
I-C4 30.0000 | 27.4457 2.5543 30.0000
N-C4 30.0000 | 1.4674 28.5326 30.0000
I-C5 20.0000 | 0.0000 20.0000 20.0000
Total 100.0000 | 48.9130 51.0870 100.0000
Note that showm does not show the flows of any compounds that are not
present in any of the streams in or out of the unit. Thus N-C5 is
left out of the displayed results.
A simple function was written to analyze a fractionator for which we
know all the mol fractions (mass fractions) in one stream and the mol
fraction (mass fraction) of one compound in the other stream. This
function was used to solve one problem in the text as seen in the
session given below. Help applied to sept gives:
>> help sept
sept: calculates the fractions to be used with frac
function frac=sept(i1,x1in2,xs1,in)
Argument Gives
i1 index of compound that is known in the exit streams
x1in2 mol or (mass) fraction of i1 in the second exit stream
xs1 composition of the first exit stream, mol or (mass) fractions
in index of the inlet stream
sept returns in frac, the fractions to be used in SEP
For additional help and picture, see PICSEPT
Example: >> ti=sept(1,.1,[0.8333 0 0.1668],5);
>> sep(ti,5,[4 3])
OKB, TYLC
Here is an image of sept.
The function sept returns the fraction of each
species in the incoming stream that goes out in the first outlet
stream. This vector then can be used with sep to
solve for the flow rates in the outlet streams. Sept
has four arguments as listed in the comments. Note that the use of
mol or mass must be consistent. If molar flowrates are used, use mol
fractions; if mass flowrates are used, use mass fractions.
Let's see how sept works by solving Example
Problem 2.8 in the text. Choose a basis of 1000 lb/hr of the
refinery stream, and let the streams be numbered as in Figure 2.8 in
the text. Since sept can have only one inlet,
streams 1 and 2 will have to be mixed. The new system will have 5
streams.
Set up cnms for the following compounds and ns with
5 streams using start301:
Component Name Formula
1 Benzene C6H6
2 Other Hydrocarbons
3 Sulfur Dioxide SO2
You have chosen to not use any compound data
If you wish to enter data for a compound, exit (control-C)
then execute "create", then run a "new session", choice (1)
Enter the number of compounds: 3
Compound names must be less than 25 characters long!
Give the name of compound # 1: benzene
Compound names must be less than 25 characters long!
Give the name of compound # 2: other hc
Compound names must be less than 25 characters long!
Give the name of compound # 3: SO2
Enter the number of streams: 5
Initialize the feed streams:
>> ns(1:2,:)=[700 300 0;0 0 3000];
Then we can mix the first two streams to form the feed stream for the
separator as stream 5:
>> mix([1 2],5)
>> showm([1 2],5,10,1)
Compound Inlet | Outlet
Stream 1 2 Total | 5
benzene 700.0 0.0 700.0 | 700.0
other hc 300.0 0.0 300.0 | 300.0
SO2 0.0 3000.0 3000.0 | 3000.0
Total 1000.0 3000.0 4000.0 | 4000.0
Choose benzene as the key compound for sept. The
composition of stream 4 is given, but the mass fraction of benzene in
stream 3 is not known. This mass fraction is probably very low since
the flowrate of SO2 is high. Let's guess that it is 0.10.
Executing sept to find the fractions for
sep:
>> ti=sept(1,.1,[.8333 0 .1667],5)
ti =
0.4870 0 0.0227
Now we know what to give sep:
>> sep(ti,5,[4 3])
>> showm(5,[4 3],12,4)
Compound Inlet | Outlet
Stream 5 | 4 3 Total
benzene 700.0000 | 340.9110 359.0890 700.0000
other hc 300.0000 | 0.0000 300.0000 300.0000
SO2 3000.0000 | 68.1986 2931.8014 3000.0000
Total 4000.0000 | 409.1095 3590.8905 4000.0000
We see that the ratio of benzene to other HC is much larger than
0.25, so we run into a trial and error situation to find the correct
value for mol fraction of benzene in stream 3. A procedure to do this
will be seen in the example illustrating the use of the secant trial
and error routine: ssec2.
The function reactr determines the reaction rates of
two reactions for a given conversion and selectivity. The eight
arguments for reactr are shown with help:
>> help reactr
reactr: calculates reaction rates for competing reactions (use with react)
rs=reactr(ipr,ipp,imr,icr,cpr,spp,in)
Argument Gives
ipr index of primary reactant,
ipp index of primary product,
imr index of main reaction,
icr index of competing reaction,
cpr conversion of primary reactant,
spp selectivity to primary product,
in index of inlet stream,
reactr returns the reaction rates to be used in REACT for rs.
For additional help and picture, see PICREACTr
Example: >> rv=reactr(4,1,1,2,0.25,0.8,1);
>> react(rv,1,2)
OKB, TYLC
Here is the illustration and example of reactr:
We will use Example Problem 3.16 in the text to illustrate the
operation of reactr. There are 6 components and 2
streams. Index the 6 components as shown in the exit stream of Figure
3.9 in the text:
Component Name Formula
1 Ethylene Oxide C2H4O
2 Carbon Dioxide CO2
3 Water H2O
4 Ethylene C2H4
5 Oxygen O2
6 Nitrogen N2
Define the names of the compounds, the reactions and the initial
ns with start301:
Input the name of your new file: test The output file name is: test Input the number of compounds: 6 The number of compounds is: 6 Here are your compounds' formulae and names: No. Formula Name ---------------------------------------- 1 C2H4O ethylene oxide 2 CO2 carbon dioxide 3 H2O water 4 C2H4 ethylene 5 O2 oxygen 6 N2 nitrogen Here are your reactions: ---------------------------------------- 1) 2C2H4 + O2 --> 2C2H4O 2) C2H4 + 3O2 --> 2CO2 + 2H2O Enter the number of streams: 2 The variables for your compounds have now been created, you may continue, or come back later and reload the same data.
Using 1000 mol/hr feed as the basis.
>> ns(1,:)=[0 0 0 100 189 711];
The primary reactant is ethylene, the primary product is ethylene
oxide, and the main reaction is reaction 1. The conversion and
selectivity are given as 0.25 and 0.8. Thus the arguments for
reactr are:
4 1 1 2 0.25 0.80 1
C2H4 C2H4O Rxn1 Rxn2 conv. selec inlet stream
Here is our solution to the example problem using the modules with our special function reactr.
>> rs=reactr(4,1,1,2,0.25,0.8,1)
rs =
10.0000 5.0000
>> react(rs,1,2)
>> showm(1,2,10,4)
Compound Inlet | Outlet
Stream 1 | 2
ethylene oxide 0.0000 | 20.0000
carbon dioxide 0.0000 | 10.0000
water 0.0000 | 10.0000
ethylene 100.0000 | 75.0000
oxygen 189.0000 | 164.0000
nitrogen 711.0000 | 711.0000
Total 1000.0000 | 990.0000