One possible approach of segmentation is to use edge detection. Assuming that regions are contained in edges, it is possible to segment an image by detecting edges and then letting everything contained by the edge contour be a region. This method turns out to be rather easy to implement and also results in good segmentation.

The steps necessary for an edge detection approach:

1. Find edges by an edge detection algorithm, ie. gradient, Laplacian or multi-scale edge detection.
2. Close gaps in the resulting edge contour to prevent regions from flowing into each other.
3. Define regions by letting the regions be the areas contained by different parts of the edge contour.
4. Eliminate edges by merging them into the most suiting region.
5. Eliminate small regions to emphasize properties of the image which you are looking for.

Edge Detection Techniques

The first step of this segmentation approach is to locate the edges. We need to find a good way to do this. Edge detection is a well researched and documented area and there are several good detectors to choose from. Some common detectors are based on the gradient, Laplacian or any of these applied at multiple scales.

Gradient Methods

The idea behind different gradient based method is that edges correspond to peaks in the gradient of an image. By assuming that a point is a possible edge point if the gradient at that point is greater than a certain threshold we get an area of possible edge points. However, this approach will yield large edge regions instead of a simple edge contour. Because of this it is necessary to perform edge thinning where you find the gradient peaks among the possible edge points.

Laplacian Methods

The Laplacian based edge detection methods are founded on the observation that edges correspond to zero-crossings of the second derivative. The big problem with this approach is that it will result in many false edges. However, this problem can be solved by looking at local variance at feasible edge points and removing edge points which have a local variance below some threshold. This method is also very sensitive to noise.

Multi-scale Edge Detection

Multi-scale edge detection is based on the fact that edges exist at different scales. In order to match all aspects of an image it is necessary to perform edge detection at multiple scales. One method resulting in a good edge contour is taking the laplacian of Gaussian at multiple scales. Here you start with performing low pass filtering with a 2D Gaussian and then you find zero crossings ot the laplacian of the result. The laplacian of Gaussian is in fact a wavelet called the Mexican Hat. This suggests that it would be a good idea to apply wavelets at multiple scales.

Image showing the results of different edge detectors applied to "Buck".

Implementation

In our implementation of a segmentation algorithm we decided to use a Sobel gradient edge detector which we implemented ourselves. It has an adaptable threshold which automaticly adjusts itself to get a possible number of edge points covering 25% of the total image. This works well in most of the cases that we have tested. A necessary step in our edge detection is edge thinning where we find the real gradient peaks among the possible edge points. Our resulting edge contour will be an image where the edges are represented by the value 255 and nonedge points are represented by 0.

The next step is to close gaps in the resulting edge contour. We have implemented a method connecting an unconnected edgepoint to the closest edgepoint by a straight line. We have also restricted the algorithm to create a connection if there is an edge point within 10 pixels from the unconnected edge. It also primarily looks for edge points in the direction of the already defined edge contour.

After closing possible gaps in the edge contour we define our regions as pixels surrounded by edges. This is done in a recursive function where we look for pixels with the value 0. When we find such a pixel we assign it an integer value starting at 256 and going up. Then we recursively "ask" the surrounding pixels if they are edge points. If not we set them to the same "color value" as the previous pixel. One problem with this implementation is that it is heavily recursive. If this method was applied to the whole image at once, Matlab's recursion limit would be exceeded and even cause Matlab to crash in certain cases. We solved this problem by applying this function to blocks of the image. Finally we merged regions not separated by edges.

As the last step in our algorithm we removed the edges by merging them into the nearby regions. We let an edge point belong to the region with the closest average pixel value.

We also implemented functions removing regions smaller than a wanted size. This function can be used to merge small regions into larger regions to get a desired resolution.

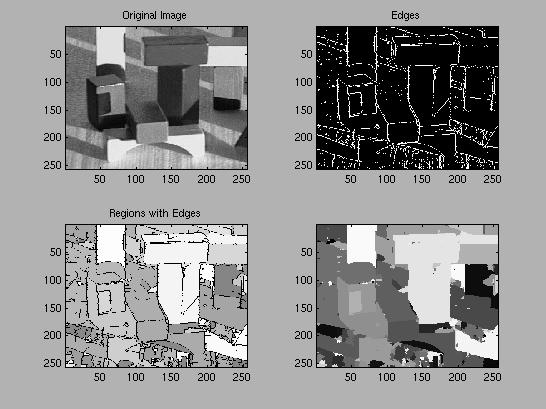
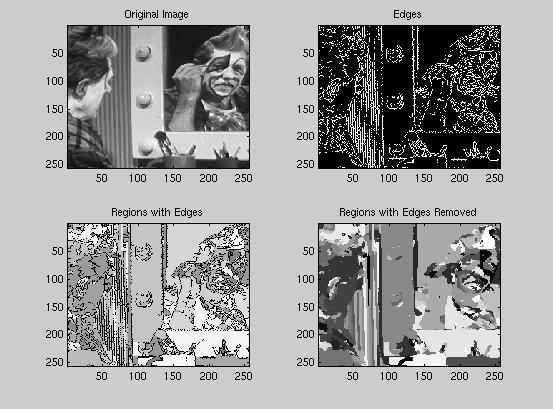
Image of "Buck" at different stages of the segmentation algorithm.

Pros and Cons of an Edge Detection Approach

1. One good aspect of edge detection is that the technique is well domented and researched. There are many different good methods to choose from and there are also several methods implemented in Matlab.
2. Since several edge detectors are implemented in Matlab it is pretty easy to complete an implementation of an algorithm for segmentation using edge detection.

1. One problem with the approach is that it is hard to design edge detectors that work well for a wide variety of images.
2. Another drawback is that it is necessary to implement an algorithm for closing the edge contours.

Possible Improvements

We have implemented a segmentaion algorithm that works rather well. However, there are several aspects of the method which could be improved. First of all the edge detection could probably be done better using wavelets at multiple scales. Another improvement would be to develop a more advanced algorithm for connection of gaps in the edge contours. Here it would be possible to try to match more advanced curvatures than straight lines.