
Figure 1 : Different background colors
Project Two - Automatic Coin Counter
* Intro *
Rusty's Group Team decided almost immediately to do our second project on feature extraction. We brainstormed a good deal about different projects, but settled on attempting to reproduce a project Angela once saw at National Instruments which counted coins. This project was appealing for a couple of reasons: we could create our own data images easily, and it is about money, which was on the minds of almost all graduating engineers this time of year.
We considered the physical setup of the problem to be that the coins run along on a conveyor belt and are filmed by a digital video camera from which frames are taken and analyzed at intervals to count the change on the belt. We did not considered our images for analysis to be non-blurred and taken from a fixed height. The first consideration in properly modeling our setup how to make sure the coins show up well on the conveyor belt. To test this we tested our ability to find edges of the coins when they were lying on differently colored backgrounds (since we were using black and white images, the intensity was the only important quality of the background). We found black and a shade of bright yellow which corresponded to an intesity of roughly 20% black and 80% white.

Once we were set on how to obtain the images and the proper background to use, we faced the issue of the type of images we would get. We decided the coins could be patterned in four possible arrangements: lying flat and isolated, lying flat and touching, overlapping, and being completely overlapped. To ease the project and the chance of getting results we removed the final two possibilities by saying our coin counting machine has a mechanical sweeper arm which makes certain the coins are only lying flat, but still possibly touching each other.
Finally, we used only the four major U.S. coins - the quarter, dime, nickel, and
penny. To summarize, we photographed single layers of coins on black and light gray
backgrounds from a fixed height with a digital camera.
* Issues we encountered *
In an effort to explore a wider variety of image processing techniques, we
decided to not use a "mask" method of coin-finding. Instead, we used edge
detection and a radius-calculating algorithm to determine the location and
value of each coin in the image. Our initial attempt at edge detection was
to use the gradient method with the Sobel row and column matricies. This
produced less than satisfactory results, which is probably because our
method was extremely simplified -- we didn't implement edge-thinning or
local thresholding. So, while we found edges well, we found all
the edges. It was too difficult to find the border edges amidst all
of the texture edges in the resulting image (see figure 2, below).
In our next attmept at edge detection, we found the zero-crossings of the
second derivative of the image (the Laplacian approach). Unfortunately, as
is the problem with Laplacian methods, this gave us every edge in the
image, even the tiniest ones. We decided to use Marr's multi-scale edge
detection method, which uses a smoothing filter to get rid of the small
edges. This result also
proved to be problematic because of the loss of resolution. Instead of
smooth, circular edges, we found sharp, jagged edges that are not
compatible with our radius-finding algorithm.
Our fourth approach was to use the wavelet-based method of multi-scale edge
detection. We scaled the image down to one-fourth of it's original size,
using the Harr wavelet. By summing the squares of the edge images in the
lower left and right and upper right quadrants of the smallest image block, we found the edges of the image at that scale.
Unfortunately, this also produced resolution problems (see figure 3).
Finally, after trying numerous techniques, we found the edge detection
functions in Matlab. Before passing our image into the edge detector, we
smoothed it using a median filter. Median filters are good for our
purposes because they smooth out small edges (the texture of the coin
surface, for example), while preserving the larger, border edges.
Comparing the results of the Matlab edge-detected images to those of our
methods, we decided to use the Matlab functions. We found that the Roberts
gradient method function worked best -- better than the Sobel or Prewitt
methods. The final edge image, smoothed with a median filter of length
eight and edge-detected with the Roberts function, is shown below
(figure 4).
Once we were able to successfully find edges, it was necessary to
determine the radius of each particular coin. We took a picture of each
coin from the same height we took the original pictures, then did edge
detection on each coin. We would start by looking down the columns until
we found an edge. This edge would correspond to the point a vertical line
would be tangent to the coin. From this point, we would fix the rows, then
look column by column until we found another edge. The distance to this
edge would be the diameter, and of course from the diameter we know the
radius. We would then reverse the process, we would look down the rows
until we found an edge, fix the column value, then traverse row by row
until the next edge is found. As long as the two radii were equal, we had
found a good value for the radius of the coin. Please refer to the functions
radius and
vertradius.
From the height we took the pictures we ran into the problem of dimes
and pennies having radii that were only one pixel different. For our
purposes, we were able to solve this problem by taking advantage of the
fact that dimes and pennies have different grayscale values, and if one was
found, we could check the grayscale. If the automatic coin counter were to
be implemented in industry or for other purposes, a better solution would
probably be to simply take the pictures from a lower height, then the
difference between the radii would be more significant, and easier to detect.
A third problem we encountered while working on this project was whether to use masking or not.
The way this technique would work would be to take an
image of a coin, and convolve this image with our original image at each
point. After convolving the two images, we would then check for pulses,
which would correspond to locations of a coin. This would have to be done
eight times, twice for each different type of coin (to account for both sides of the coin). Although we knew
this solution would work, we chose not to implement it for two reasons.
First, becuase a group a couple of years ago did a very similar project
using masks, and second because we felt that other solutions would expose
us to more digital image processing techniques. We are not sure if this
solution would have been more elegant than our own, but by not using this
technique we were able to do more original work, and learn more at the same
time.
* Implementation *
In our final coin-counter implementation, we first took the original image and smoothed it using a median filter. A median filter is an ideal solution to our smoothing problem because it preserves big edges while smoothing out small and impulsive ones. This was done using the function medfilt, which implements a median filter and takes in the length of the filter as an argument (in our case, we used a window of size 8).
Once we have this smoothed image, we ran it through our coin-counter, coincount. This coin-counter first performs edge detection on the smoothed image using Matlab's built-in edge detector. Next, it looks through the whole image pixel by pixel.
At each pixel, it checks in eight directions for edges (center). If it finds more than a certain threshold number of edges that are of the same length from the center pixel, it will mark that pixel as a possible center and perform checks in eight more different directions for that radius (checkmore). If within the entire set of sixteen checks, the number of hits exceeds a certain threshold, it will declare that pixel as the center of a certain type of coin.
Once we have run through the entire image, we now have a map of where all the coin centers are. However, since our methods are discrete, we need to account for slight inaccuracies in center-finding. In other words, one coin may produce a small cluster of centers that will pass the required parameters. As a result, we use the function checkaround, which looks at blocks of pixels and counts a cluster of centers as only a single center.
* Results *
We tried the method we described above on the following coins images. This image contains a single layer of assorted coins.
In order to minimize the number of internal coin edges, we first median-filtered the image using a filter of length 8.
Next, we performed edge detection on the image using the built-in Matlab edge detector: edge(image,'roberts');
Once we have this set of edges, we ran our coin-counting algorithm on this image. The result? Which is exactly the amount of change in the image.
* Conclusion *
Rusty's Group Team was satisfied with the final performance of our coin counter.
Although, our implementation was specific to the problem of finding and counting coins,
we got some much needed practical experience with image processing and were able to
learn about multiple techiniques and strategies. The thrill that was associated with
our counter actually returning $.47 cannot properly be explained in this report.
A special group thanks goes out to Jamie Liang who provided the digital camera and
download software which allowed us to easily create our images. Although Jamie knows
next to nothing about digital image processing, he is a fine break dancer. We
encourage you to visit his
breakdancing website
filled with many excellent pictures taken
with the same camera and utilizing the same software package.
Best Regards,

Figure 2 : Our implementation of an edge detector
Figure 3 : Wavelet-based scaling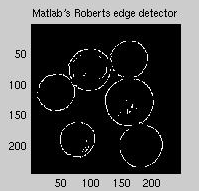
Figure 4 : Matlab's built-in edge detector
Figure 5 : Original coins image
Figure 6 : Median-filtered image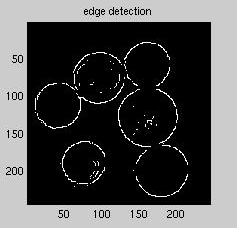
Figure 7 : Edge detection on smoothed image
Angela Chau
Mike McClintock
Kristen Murray
J Provine