Understand the IFS in 5 easy minutes
Fractal image compression is based on concept of an Iterated Function System.
Thus, it is important to understand the Iterated Function
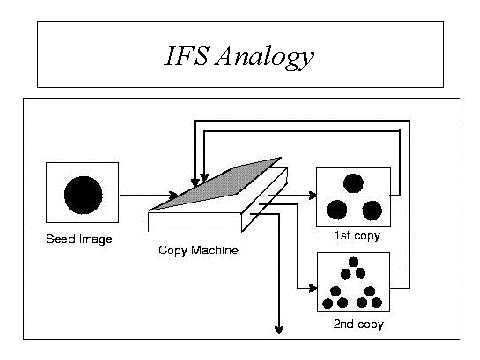
System(IFS). The copy machine in the picture accepts an image as an
input. It then produces 3 small copies of the input image. The copy
machine arranges the small copies in a triangle.
The ouput of the copy image is then fedback into the input. This is known
as a unity feedback system. The second output of the system is then fed
back into the input again. The second output is shown in the picture as
well. If the output of the system is repeatedly fed back into the system,
the output will be as shown below.

The final output of the copy machine is called the attractor. The attractor
above is called the Sierpinski triangle. It is a fractal.
The copy machine in the first figure accepted a circle as the first image.
However the final output (attractor) only depends on the fact that the copy
machine arranged the outputs in a triangle formation. If the initial image
had been a square or a hexagon, the final output(attractor) would have
still been the same Sierpinski triangle. ANY INITIAL PICTURE WOULD GIVE THE
SAME FINAL IMAGE(ATTRACTOR)
Now for the fun fact. Let us say that we wanted to store a picture of the
Sierpinski triangle. It is a fractal image. We could store it as a jpeg,
gif etc. However we are now smarter than that. We could simply store the
set of transformations used to generate it. The transformation went
something like this. "Make 3 small copies of it and put them in an
equilateral triangle". All we have to do to generate the Sierpinski
triangle, is to repeatedly apply the transformation to any input image (
box, circle, whatever). This will generate the Sierpinski triangle
perfectly. The image compression is huge, since you are only storing a few
coefficients representing the transformation.
Purely fractal images like the Sierpinski triangle can be compressed with
great efficiency. We now turn to every everyday images ( people, trees,
dogs etc). It turns out that these images have some fractal structure to
them. Thus it may be possible to store a set of transformations to represent
them. In practice, fractal coders look for sets of transformations that
link one part of the image to another. These transformations and the
location of the blocks that relate to each other are all that is stored.


