To date, no precise definition exists that includes all sets considered to be fractals. Instead, there are certain properties that can be used to classify a set as a fractal. We consider a set F to be a Fractal if it has detail at every scale, is (exactly, approximately, or statistacally) self-similar, and can be described by a simple algorithm. An example of a fractal is shown below.

Fractal Image Compression
When a contractive mapping (one that moves points closer together) of the 2D plane is iteratively performed on an arbitrary image, with the output of each step being used as the input for the next iteration, the output will converge to a unique fixed point that is independent of the original input image. Such a transformation is refered to as an iterated function system (IFS), and the fixed point is known as the attractor of the IFS. The attractor, being composed of succesive mappings of itself, has detail at every scale, and is refered to as a fractal.
The idea of encoding images as fractals was first brought up by M. Barnsley.
He noticed that IFSs could be used to generate complex, natural looking
images, and he posed the idea of working backwards from a given image to
determine an IFS that defines it. Fractal image coders are based on these
ideas. These coders rely on the existance of an IFS whose attractor is
the image. Very high compression is achieved by storing the coefficients
of the IFS instead of the image pixels. The image is then decoded by iterating
the IFS to it's attactor. Three basic problems have been the focus of study
on fractal image compression:
One advantage of fractal image compression over traditional transform coding is that fractal compression takes advantage of local scale invariance. Several natural image features such as, straight edges and constant regions are unchanged by rescaling. This type of redundancy is not exploited by traditional image coders, and this is the main motivation for fractal image coding. The first fractal based image coder was described by Jacquin in 1990.
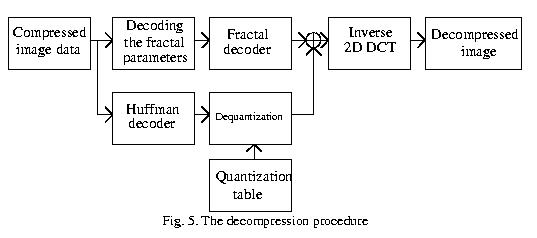
After the initial paper introduced by Jaquin, several variations of fractal block coders have been proposed. What we have found in the literature is that although pure fractal block coding achieves high compression, the quality of the decompressed images is not very good. An interesting area of study is hybrid image coders based on transform coding and fractal image compression. These methods have been shown to give appreciable improvement in image quality, and better compression than tranform coders. One such coder proposed by Zhao and Yuan combines the discrete cosine transform and block-based fractal coding. This project demonstrates a Matlab based implementation of this image coding system.
A DCT and Fractal Block Coding Based Image Codec
In the coder described by Zhao and Yuan, the discrete cosine transform is first performed on the image to be compressed. The transform coefficients are then encoded using fractal block coding, producing a set of affine transformations of which the DCT representation is an approximate attractor. A unique feature of this method is that in addition to storing the IFS, the differences between the original and approximate images are also stored, and used to increase PSNR. Below is a diagram of the compression scheme that we will attempt to implement.
The DCT transform is applied to 8X8 blocks of the image which become the range blocks for the fractal encoding stage. Rather than fractal coding every 8X8 block, the coder performs a classification of the blocks to determine their relative complexity and selects blocks to be coded. The blocks are classified based on the three DCT coefficients surrounding the origin. The following equation is used to classify a block as a high activity block or a low activity block:
EQUATION
If a block is smooth in the spacial domain, it's AC coefficients are small and do not contribute much to the percieved image quality. Accordingly, the above equation will yield a small value when applied to these spacially smooth blocks. These blocks are then classified as low activity blocks, and only their DC components are coded. The remaining blocks are classified as high activity blocks, and they constitute the range blocks of the fractal block coding stage. The entire spectral content of each range block is encoded as a set of affine transformations. The threshold (T) in the above equation provides a convenient "knob" for tuning the trade-off between compression ratio and image quality. If the threshold is increased, fewer high activity blocks are identified, and the compression ratio increases, while image quality decreases. Conversly, lowering the threshold creates more high activity blocks, thereby increasing image quality, and the number of bits required for the representation.
The set of domain blocks for the fractal block coding scheme is obtained by performing the DCT transform on 16x16-pixel blocks of the image. The center of adjacent domain blocks are 8pixels apart, so that each block is overlapped with all of it's adjacent neighboring blocks. This yields a set of 30x30=900 domain blocks, used to perform the fractal encoding.
The next step in the coding process is the fractal encoding of each range block. This stage of the coder is extremely compute intensive, and gives rise to the long coding delays common to fractal block coders. For each range block, a search of the entire set of domain blocks is preformed to find the domain block that is most similar to the range block. The process is shown in pseudo code below;
for each range block {Frange(u,v)}
for each domain block {Fdomain(u,v)}
compare(Frange, T.Q.Fdomain)
end
end
The inner loop is the search to find the domain block, T transformation, and Q transformation that yield the closest comparison, measured in mean square error. The Q is a contractivity operator, that maps the domain block to the 8x8 range block. The T is a compund transformation that consists of an isometry, a scaling, and a luminance shift.
....