
Introduction to Transform Coding
One dimensional signals are usually represented in terms of a set of basis
functions. The Fourier transform has cosinusoids as its basis functions.
We can expand the concept of transforms to 2 dimensions. An image can be
represented in terms of a set of arrays called basis images.
The purpose of image coding is to represent the image with a fewer number
of bits, while maintaing the visual quality of the image. Image transforms
have been widely used to implement image coders. Image transforms are
useful for coding, since images generally have a compact representation in
the transform domain.
An image transform takes N*M pixel values in an image and transforms them
into N*M transform values. The original image has its energy spread
throughout the image. This means that the large pixel values are likely to
be anywhere in the image. A "good" transform has a high degree of energy
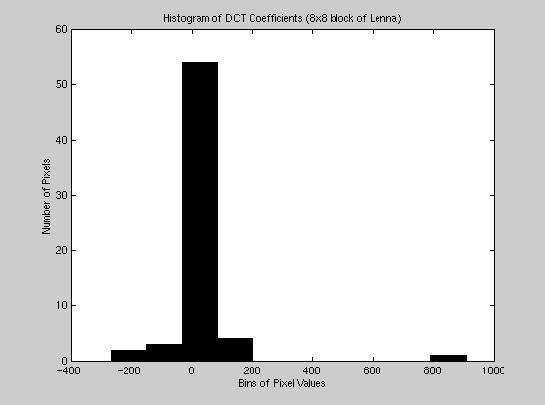
compaction. The large transform values are localized. The histogram of
pixel values illustrates the fact that most pixels have very low values and
a few pixels have large values. A large number of
bits are allocated to these few transform coefficients. Very few bits are
allocated to the small transform values. Thus most of the information in
the image can be represented by a smaller number of total bits.
The compressed image can be obtained by applying the inverse transform to
the transform values. The optimal transform is the one that
minimizes the distortion between the original and compressed images. This
transform is the Karhunen-Loeve transform. However the Karhunen-Loeve
transform requires knowledge of the second order statistics of the image
and is very difficult to implement. Since the second order statistics of
the image are difficult to obtain, approximations to the Karhunen-Loeve
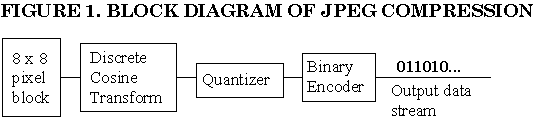
transform are preferred in practice. One of these is the Discrete Cosine
Transform (DCT). The DCT is a fast transform with complexity of
O(NlogN). It gives real values which correspond to the frequency content of
the signal. It works extremely well with highly correlated data. One versionof the DCT is implemented in the popular JPEG
compression scheme. The wavelet transform is another excellent transform
for image coding. Its results are closer to that of the K-L transform than
the Discrete Cosine Transform.
Back..


