Tomographic reconstruction using algebraic techniques is complicated by the presence of noise in the collected data much in the same way as the filtered back projection method. Within this project, we have investigated two alternative filtering methods for suppressing the effects of this noise.
First, we investigated the possibility of including a Wiener filter as the constraining operator in the minimization problem (17), as derived by Jain [5] and Castleman [1]. As shown by these authors, the resulting equation is
Here, 
is the noise-to-signal ratio, and
is the inverse of the autocorrelation matrix for the
image. Since the matrix R is the same size as 
, it is not
feasible to compute the inverse of this matrix exactly. We therefore
attempted to approximate by a sparse matrix retaining only
the largest coefficients. This approximation resulted in a matrix Q
similar to that used for the Laplacian smoothing constraint described
by Castleman [1]. We were unable, however, to obtain
useful results with this method, presumably due to errors introduced
in approximating the matrix.
We turned therefore to a method similar to that used for the filtered back-projection, where the projection data were 1-D filtered using a Wiener smoothing filter based upon the same image model as in the filtered back-projection method. For this method, however, the required filter is simply a lowpass filter, given by
since the ramp portion of the Wiener filter used for filtered back-projection is a part of that particular reconstruction method. The frequency response of the lowpass filter used for the algebraic technique is shown in Fig. 10, along with the resulting reconstructed image.
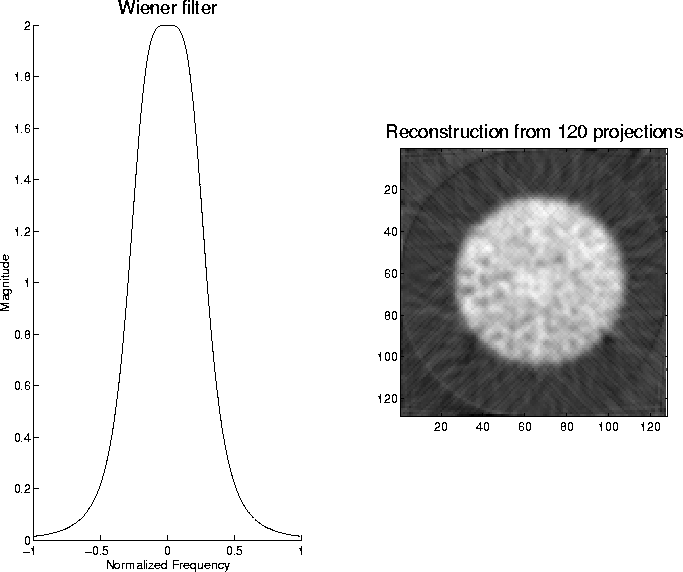
Figure 10: The frequency response of the Wiener filter used for the
algebraic reconstruction method (left), and the resulting
reconstructed image (right).