![]()
Basics of HOS
Higher order statistics have the advantage of containing information regarding deviations from Gaussianity and true phase of the linear systems. They are also capable of detecting and characterizing the non-linearity of the processes. They have many applications in different areas of signal processing including but not limitted to array processing, pattern and signal classification, harmonic retrieval, blind deconvolution and equalization.
In this project, we have used in particular the third order statistics (3rd order cumulant and bispectrum) to model the real-world textures.
The main motivations for the use of higher order spectra include:
Moments
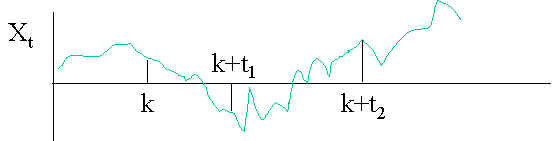
Similar to second order moment, the third order moment is defined as the ensemble average of the product of three time instants of the random process.
![]()

In general, moments of a random process are obtained from the moment generating function. The moment generating function is defined as
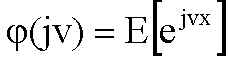
Moments are the coefficients of powers of (jv) in the Taylor series expansion of this generating function.
Cumulants
The cumulant of a random process is obtained from cumulant generating function, which is defined as the Log of the moment generating function mentioned above.
Interestingly, for orders less than or equal to three, cumulants of a random process are equal to central moments of the same order. For Gaussian prcesses, it turns out that all cumulants are zero for orders greater than two.
Cumulant Spectra
Cumulant spectra are the Fourier transforms of cumulants. A particular case of higher order spectra is the third-order spectrum which is called Bispectrum and is defined as the Fourier transform of the third order cumulant.
Symmetrical properties
The third order cumulant of a random process has a 6-fold symmetry. This results in a 6-fold symmetry for its Fourier transform, bispectrum. Moreover, if the process is real, the conjugate symmetry of the Fourier transform, provides 6 additional symmetries. So, for the case of real prcesses, the bispectrum has a 12-fold symmetry formulated in the following equations

Non-redundant region
The non-redundant region of a cumulant or bispectrum is defined as a subset of the support of the function which suffices to calculate the function in the whole region. These are defined using the symmetrical properties explained above.
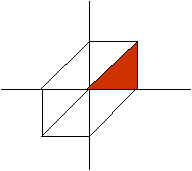
A non-redundant region of the third order cumulant
We take advantage of the symmetrical properties of the bispectrum to reduce the computational complexity and memory requirements of calculating third order statistics.