
COMP 210: Principles of Computing and Programming |
Lecture #16 Fall 2003 |
 |
|
When trying to model genealogy before, we focussed on the invariant that children have parents. But sometimes it is better to model a genealogy the other way around, that is to model people as having children:
;; A Person is a structure
;; where name is their name, year is their birth year
;; and kids is a list the person's children.
;; (make-Person symbol num list-of-Persons)
(define-struct Person (name year kids))
The use of a list for the children enables to model the varying numbers of children a person might have. An empty kids list thus means that the person has no children.
This data structure gives rise to a function template:
;; Template for Person
(define (f-Person a-person)
...(Person-name a-person)...
...(Person-year a-person)...
...(f-lop (Person-kids a-person))...)
Note that the template preserves the encapsulation of the kids list by calling another function to process it.
So, what is this list-of-Persons, anyway?
;; A list-of-Persons is either
;; - empty
;; - (cons Person list-of-Persons)
The template is what you'd expect it to be:
;; Template for list-of-Persons
(define (f-lop a-lop)
(cond
[(empty? a-lop) ...]
[(cons? a-lop) ...(f-Person (first a-lop))...(f-lop (rest a-lop))...)]))
Once again, the encapsulation of the Person
structure in first is respected.
So what have we here?
Kinda circular ain't it?
A set of data structures that are recursive via each other are called "mutually recursive data structures".
The UML diagram for the above data structures looks like this:
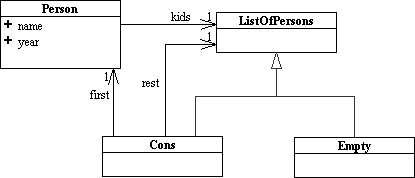
Notice how the composition relationships form a circle (via the inheritance from ListOfPersons to Cons).
.Let's build some people. Let's see how the Simpsons looks modeled this way:
(define Bart (make-Person 'Bart 1979 empty))
(define Lisa (make-Person 'Lisa 1981 empty))
(define Maggie (make-Person 'Maggie 1988 empty))
(define Homer (make-Person 'Homer 1955 (list Bart Lisa Maggie)))
(define Marge (make-Person 'Marge 1956 (list Bart Lisa Maggie)))
(define Selma (make-Person 'Selma 1950 empty))
(define Patty (make-Person 'Patty 1950 empty))
(define Jackie (make-Person 'Jackie 1926 (list Selma Patty Marge)))
(define Herbert (make-Person 'Herbert 1950 empty))
(define Mona (make-Person 'Mona 1929 (list Herbert Homer)))
(define Abe (make-Person 'Abe 1920 (list Herbert Homer)))
If you were to display Abe, you'd see something like this (this has been pretty-fied a bit):
(make-Person 'Abe 1920
(list (make-Person 'Herbert 1950
empty)
(make-Person 'Homer 1955
(list (make-Person 'Bart 1979
empty)
(make-Person 'Lisa 1981
empty)
(make-Person 'Maggie 1988
empty)))))
All right, let's write some functions!
How about a function to count all the descendents in a tree? Just follow the yellow template road...
(Remember: delegate, delegate, delegate!)
;;countAll: Person --> num
;; counts all the persons in the tree
(define (countAll person)
(+ 1 (countAll_lop (Person-kids person))))
;; countAll_lop: list-of-persons --> num
;; counts all the persons in a list-of-persons
(define (countAll_lop lop)
(cond
[(empty? lop) 0]
[(cons? lop) (+ (countAll (first lop))
(countAll_lop (rest lop)))]))
"countAll test cases:"
(= 1 (countAll Bart))
(= 4 (countAll Homer))
(= 7 (countAll Jackie))
You gotta love it.
Ok. So much for the easy stuff. How about something a little more challenging?
How about a function that returns a list of names of descendents that have
at least n children?
Let's look at the function on the Person first. Bascially, if
a Person's name is to be included on the list, then they have
to have at least n children. So we pretend that we've already
written a function that counts the number of children. We write a function
that creates a list with the Person's name in it if they have
more than n kids, and an empty list if they don't:
;; atLeastNKids: Person num --> list-of-sym
;; Returns a list of names of all descendents, including the person,
;; who have at least n kids.
(define (atLeastNKids person n)
(... (cond
[(<= n (countKids (Person-kids person))) (list (Person-name person))]
[else empty])
...))
The function to count the number of Persons in a list-of-Persons
is trivial:
;; countKids: list-of-Persons --> num
;; counts the number of Persons in the list.
(define (countKids a-lop)
(cond
[(empty? a-lop) 0]
[(cons? a-lop) (+ 1 (countKids (rest a-lop)))]))
But now what? If we knew the list of names of people with at least n kids
from the kids list, then all we'd have to do is to append that list to the
list we created above that either has our Person's name in it,
or is empty. Once again and as per the templates, we assume that there's a
neat-o function on a list-of-Persons
that will do just what we want:
;; atLeastNKids: Person num --> list-of-sym
;; Returns a list of names of all descendents, including the person,
;; who have at least n kids.
(define (atLeastNKids person n)
(append
(cond
[(<= n (countKids (Person-kids person))) (list (Person-name person))]
[else empty])
(atLeastNKids_lop (Person-kids person) n)))
atLeastNKids_lop is straightforward--all it does is call atLeastNKids
on each Person (see the mutual recursion here?) in the list and
append all the results together:
;; atLeastNKids_lop: list-of-Persons num --> list-of-sym
;; Returns the list of all descendents, including all Persons in the list,
;; who have at least n children.
(define (atLeastNKids_lop lop n)
(cond
[(empty? lop) empty]
[(cons? lop) (append (atLeastNKids (first lop) n)
(atLeastNKids_lop (rest lop) n)) ]))
No problem. Here are some test cases that I wrote long time ago, of course ;-)
"atLeastNKids test cases:"
(equal? (list 'Bart) (atLeastNKids Bart 0))
(equal? empty (atLeastNKids Bart 1))
(equal? (list 'Homer) (atLeastNKids Homer 1))
(equal? (list 'Jackie 'Marge) (atLeastNKids Jackie 2))
(equal? empty (atLeastNKids Jackie 4))
(equal? (list 'Homer) (atLeastNKids Abe 3))
This "Let's See What We've Got To Do" analysis seemed to work ok. It's very useful, I think. I use it a lot.
Well, that was cool. But not cool enough...
Now you may ask, "Why do I need to traverse the kids list twice? Couldn't I figure out all my decendents that have enough kids and figure out if I have enough kids all on the same traversal of the kids list?"
What would such a function entail? Let's think about it here by doing a Process Flow Analysis. As it usually is, the Process Flow Analysis is dictated by a path where one is delegating to another function so as not to violate encapsulations:
atLeastNKids operates on a Person. But since
the number of kids is determined by the list of kids, then we delegate everything
to it (atLeastNKids_lop), passing our name in case it is needed.
The minimum number of kids needs to be passed too, obviously. atLeastNKids_lop
may need additional parameters, so we'll leave that up in the air for now.(define (atLeastNKids2 aPerson N)
(atLeastNKids2_lop (Person-kids aPerson) N ... (Person-name aPerson))
or more generically:
(define (f-Person aPerson ...)
...(Person-name aPerson)...(f-lop (Person-kids aPerson) ...)...)
Note that this does not preclude using the person's name as an input
to the function on a list of Persons.atLeastNKids2_lop
(define (f-lop aLoP ...)
(cond
[(empty? aLoP) ....]
[(cons? aLoP) ...(f-Person (first aLoP) ...)...(f-lop (rest aLoP)...)...]))
empty case first: This means that there
are no kids. Thus if
first and
rest) of the cons data type. Let's look down
each branch: first branch: Preserve encapsulation, so delegate
to atLeastNKids to find out who in that Person tree
has sufficient kids.rest branch: Preserve encapsulation again, this time
by recurring. Since we know that we have at least one kid, then
the minimum number of kids for rest is N-1.
Do you see how counting down N effectively counts the number of
kids? We have sufficient kids if N
passes through zero, but note that the inductive case never cares
about that. This is very similar to a function on a natural number
except that we don't stop at zero. Note that we still need to remember
the original size of N,
so we want to count down an accumulator that is initialized to N.
We'll call this accumulator, "n".first
branch in front of the result of the rest branch (this
puts the parent's name first if it is there) and we are done!atLeastNKids2_lop is thus:
(define (atLeastNKids2_lop lop N n name)
(cond
[(empty? lop) ...name...N...n...]
[(cons? lop) ...(atLeastNKids (first lop) N)
...(atLeastNKids_lop (rest lop) N (sub1 n) (first lop))...]))
So let's write a mutually recursive function of two non-trivial arguments using natural numbers. That must be worth something in Scheme-heaven!
The code follows our Process Flow Analysis exactly:
;; atLeastNKids2: Person num --> list-of-sym
;; Returns a list of names of all descendents, including the person,
;; who have at least N kids.
(define (atLeastNKids2 person N)
(atLeastNKids2_lop (Person-kids person) N N (Person-name person)))
;; atLeastNKids2_lop: list-of-Persons num num sym --> list-of-sym
;; Returns a list of names of Persons who have at least N kids.
;; The parent is included at the front of the list if the list-of-Persons
;; contains at least n Persons.
(define (atLeastNKids2_lop lop N n parent)
(cond
[(empty? lop)
(cond
[(<= n 0) (cons parent empty)]
[else empty])]
[(cons? lop)
(append (atLeastNKids2_lop (rest lop) N (sub1 n) parent)
(atLeastNKids2 (first lop) N))]))
Ta da!!
Notice how the number of kids is used both to make the mutually recursive
call to each kid (N) as well as being counted down to see how
many kids there are (n).
The backwards append (w.r.t. atLeastNKids_lop) is to get the
name of the parent to be in the list before the kids names since the determination
of whether or not to include the parent is not made until after the whole
list of kids has been processed..
Sweet!!
The code for today's lecture can be downloaded here: descendent.scm
©2003 Stephen Wong