Lecture 24: Accumulators

1. Making change:

   #|
      changer : (listof N) N -> (listof N)
      (define (changer actual-coins amount) ...)
      
      Assumption: actual-coins is sorted in descending order
   
      Purpose: produce a sub-list of actual-coins that represents amount
       the "coins" on the output are in the same order as those in 
       actual-coins
   
      Examples: 
   
       (changer (list 25 25 10 10 10 10 5 1 1) 55)
       =
       (list 25 25 5)
   
       (changer (list 25 25 10 10 10 10 5 1 1) 65)
       = 
       (list 25 25 10 5)
   |#
   
   (define (changer actual-coins amount)
     (cond
       ((and (empty? actual-coins) (= amount 0)) empty)
       ((and (cons? actual-coins)  (= amount 0)) empty)
       ((and (empty? actual-coins) (> amount 0)) ?????)
       (else (cond
   	    [(< amount (first actual-coins)) (changer (rest actual-coins) amount)]
   	    [else ; (<= amount (first actual-coins))
   	      (cons (first actual-coins) 
   		(changer (rest actual-coins) (- amount (first actual-coins))))]))))
   

   What is different about this function? -- It does not recur on the structure of the second argument! Instead, the second argument represents how much we have changed, starting from the original.

   (changer (list 25 25 10 10 10 10 5 1 1) 55)
   =
   (cons 25 (changer (list 25 10 10 10 10 5 1 1) 30))
   =
   (cons 25 (cons 25 (changer (list 10 10 10 10 5 1 1) 5)))
   =
   (cons 25 (cons 25 (changer (list 10 10 10 5 1 1) 5)))
   =
   (cons 25 (cons 25 (changer (list 10 10 5 1 1) 5)))
   =
   (cons 25 (cons 25 (changer (list 10 5 1 1) 5)))
   =
   (cons 25 (cons 25 (changer (list 5 1 1) 5)))
   =
   (cons 25 (cons 25 (cons 5 (changer (list 1 1) 0))))
   =
   (list 25 25 5)
   

   
   
   
2. Traversing a cyclic graph.
   Let's add one edge to the graph from the previous lecture: This graph is cyclic. Specifically, we can leave B and return to it, i.e., we go
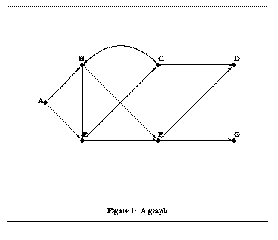
   from B to E,
   from E to C, and back
   from C to B.

   Here is a representation of this new graph:

   (define Graph-cycle
     '((A (B E))
       (B (E F))
       (C (B D))
       (D ())
       (E (C F))
       (F (D G))
       (G ())))
   

   The only difference between Graph and Graph-with-cycle is that the latter contains B as a neighbor of C.

   Our plain old find-route program won't work anymore:

     (find-route 'A 'D Graph-cycle)
   = (find-route 'B 'D Graph-cycle)
   = (find-route 'E 'D Graph-cycle)
   = (find-route 'C 'D Graph-cycle)
   = (find-route 'B 'D Graph-cycle)
   

   Since the first neighbor of A is B, the algorithm attempts to find a path that leads through B. Unfortunately, the path that starts from B contains the above cycle, and therefore the program never terminates.

   What to do? Hint: use an accumulator.

   We can introduce an "accumulator" argument that keeps track of what origination nodes the algorithm has visited. Then, when it discovers a cycle, the attempt to find a route has failed.

   (define (find-route O D graph visited)
     (cond
       ((eq? O D) (list D))
       ((member O visited) #f)
       (else (local ((define route
   		    (try-all-neighbors (neighbors O graph) D graph (cons O visited))))
   	    (cond
   	      ((boolean? route) #f)
   	      (else (cons O route)))))))
   
   (define (try-all-neighbors lo-Os D graph visited)
     (cond
       ((empty? lo-Os) #f)
       (else (local ((define route (find-route (first lo-Os) D graph visited)))
   	    (cond
   	      ((boolean? route) (try-all-neighbors (rest lo-Os) D graph visited))
   	      (else route))))))
   

   And yes, the new definition works:

    (find-route 'A 'D Graph-cycle empty)
    =
    (list 'A 'B 'E 'C 'D)
   

   Let's wrap it up in a local:

   (define (find-route O D graph)
     (local ((define (find-route O D visited)
   	    (cond
   	      ((eq? O D) (list D))
   	      ((member O visited) #f)
   	      (else (local ((define route
   			      (try-all-neighbors (neighbors O graph) D (cons O visited))))
   		      (cond
   			((boolean? route) #f)
   			(else (cons O route)))))))
   
   	  (define (try-all-neighbors lo-Os D visited)
   	    (cond
   	      ((empty? lo-Os) #f)
   	      (else (local ((define route (find-route (first lo-Os) D visited)))
   		      (cond
   			((boolean? route) (try-all-neighbors (rest lo-Os) D visited))
   			(else route)))))))
       (find-route O D empty)))
   

   
   
   
3. Accumulator arguments can be used for both functions based on structural recursion and generative recursion. What do they do? What do they have in common?