Lecture 18: Eureka!

1. readings: will hand out new readings after spring break
2. homework: only homework 6 is due on the week after spring break

   ---

   
   
   
3. let's sort numbers again:

    
   			(list 11 8 14 7)
   split:           (list 8 7) 11 (list 14)
   sort each list:  (list 7 8) 11 (list 14)
   juxtapose them:  (list 7 8 11 14)
   

   
   
   
   

   What's the basic idea?

   1. split the list into two parts:
      those larger than the first item and those smaller than the first one
   2. sort each of these two lists
   3. juxtapose the sorted lists

   Here is the complete picture:

   (list 11 8 14 7)
   (list 8 7) (list 7) empty 7 empty (list 7) 8 empty (list 7 8)	11	(list 14) empty 14 empty (list 14)
   (list 7 8 11 14)

   
   
   
   

   Okay let's try a larger example by hand:

    
   (list 33 1 9 88 77 21 20 19 87 86 99 0)
   

   Figure out on your own what's going on.
   
   
4. Let's define this program:

   ;; quick-sort : (listof number) -> (listof number)
   ;; Purpose: sort a list of numbers
   (define (quick-sort alon)
     (cond
       ((empty? alon) empty)
       (else (append 
   	    (quick-sort (smaller-items alon (first alon))) 
   	    (list (first alon)) 
   	    (quick-sort (larger-items alon (first alon)))))))
   
   ;; smaller-items : number (listof number) -> (listof number) 
   ;; Purpose: filter out that list of numbers from alon that are smaller than th
   (define (smaller-items th alon) ...)
   
   ;; larger-items : number (listof number) -> (listof number) 
   ;; Purpose: filter out that list of numbers from alon that are larger than th
   (define (larger-items th alon) ...)
   

   The last two are just like demands-going-up and demands-going-down

   What's different about this program? How does it differ from, say, insertion sort?

   
   It does not use first and rest to pick the pieces on where to recur
   even though its argument is a list. Instead, we create a whole new list.
   
   

   ---

5. Here is something I would like to be able to draw:

   And here is yet another example of this kind:

6. The crucial step in the triangle sequence is:

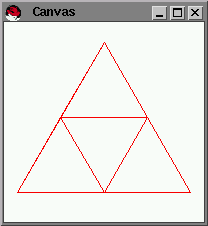
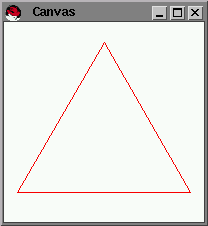
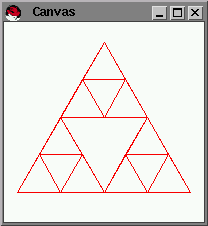
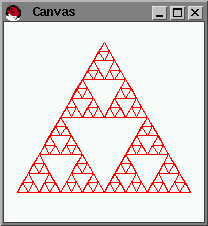
   The basic idea:

   1. pick three points
   2. draw the triangle for the three points
   3. pick the mid-points for each of pair of points
   4. start over

   Here we go:

   ;; sierpinski : posn posn posn -> #t
   ;; Purpose: draw a sierpinski triangle down to a certain size
   (define (sierpinski a b c)
     (cond
       ((too-small? a b) #t)
       (else 
         (local ((define a-b (mid-point a b))
   	      (define b-c (mid-point b c))
   	      (define c-a (mid-point a c)))
   	(and
   	  (draw-triangle a b c)	    
   	  (sierpinski a a-b c-a)
   	  (sierpinski b a-b b-c)
   	  (sierpinski c c-a b-c))))))
   
   ;; draw-triangle : posn posn posn -> #t
   ;; Purpose: draw the triangle determined 
   (define (draw-triangle A B C) ...)