Assignment 7: Generative Recursion: Basic Exercises

Before you tackle the homework, remind yourself of our General Advice, Advice on Homeworks, and Grading Guidelines. Above all, keep your work neat and honest.

1. (3pts) 28.2.7 Develop the program merge-sort, which sorts a list of numbers in ascending order, using two major auxiliary functions:
   1. The first one, make-singles, constructs a list of one-item lists from the given list of numbers. For example,

        (make-singles (list 2 5 9 3))
      = (list (list 2) (list 5) (list 9) (list 3))
      

   2. The second merge-all-neighbors merges pairs of neighboring lists. More specifically, it consumes a list of lists (of numbers) and merges neighbors. For example,

        (merge-all-neighbors (list (list 2) (list 5) (list 9) (list 3)))
      = (list (list 2 5) (list 3 9))
      

      In general, this function yields a list that is approximately half as long as the input. Why is the output not always half as long as the input?
   Make sure to develop the functions independently. The second one, merge-all-neighbors, is based on generative recursion and is used as the generative step in the main auxiliary function for merge-sort.

   ---

2. (3pts) 30.1.5 Take a look at the following two pictures: The left one is the basic step for the generation of the ``Savannah'' tree on the right. It is analogous to the middle picture in the series of triangles shown at the beginning of this section. Develop a program that draws trees like the one in the right picture. Hint: Think about the generation as drawing straight lines and as following new directions given in angles (radians). Note: Some knowledge about sin and cos are helpful.

   ---

3. (4pts) 30.3.6 As mentioned in section 26, mathematicians are not only interested in the roots of functions, but also in the area that a function encloses between two points. Take another look at the following graph:

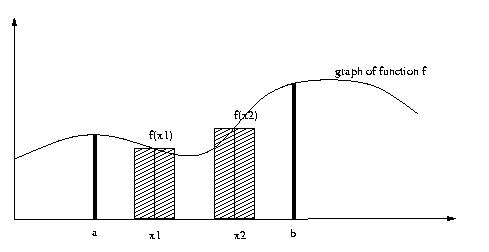
   Here the area of interest is that enclosed by the bold vertical lines at a and b, the x-axis, and the graph of the function.

   In section 26, we learned to approximate the area by computing and adding up the area of rectangles like the two above.

   Based on our use of divide and conquer (bi-section in math-speak), it is easy to design an algorithm (i.e., a program based on generative recursion) that computes the area. Roughly speaking, we split the interval into two pieces, compute the area of each piece, and add the two areas together.

   Step 1: Develop the algorithm integrate-dc, which integrates a function f between the boundaries left and right via the divide-and-conquer strategy employed in find-root. Use rectangle approximations when an interval has become small enough.

   Although the area of a rectangle is easy to compute, a rectangle is often a bad approximation of the area under a function graph. A better geometric shape is the trapezoid limited by a, (f a), b, and (f b). Its area is:

                       f(right) - f(left)
      (right - left) * ------------------
                                2
   

   Step 2: Modify integrate-dc so that it uses trapezoids instead of rectangles.

   The plain divide-and-conquer approach is wasteful. Consider a function graph is level in one part and rapidly changes in another. For the level part it is pointless to keep splitting th interval. We could just compute the trapezoid over a and b instead of the two halves.

   To discover when f is level, we can change the algorithm as follows. Instead of just testing how large the interval is, the new algorithm computes the area of three trapezoids: the given one, and the two halves. Suppose the difference between the two is less than

    TOLERANCE * (right - left) 

   This area represents a small rectangle, of height TOLERANCE, and represents the error margin of our computation. In other words, the algorithm determines whether f changes enough to affect the error margin, and if not, it stops. Otherwise, it continues with the divide-and-conquer approach.

   Step 3: Develop integrate-adaptive, which integrates a function f between left and right according to the suggested method. Do not discuss the termination of integrate-adaptive.

   Note: The algorithm is called ``adaptive integration'' because it automatically adapts its strategy. For those parts of f that are level, it performs just a few calculations; for the other parts, it decreases the interval a lot so that the error margin is also decreased accordingly