Spring 1996
Induction is a technique, demonstrated in the last two lectures, for proving infinitely many propositions at once. For instance, recall the definition
![]()
Suppose that we want to prove the claim
![]()
That represents infinitely many equations, including the following:
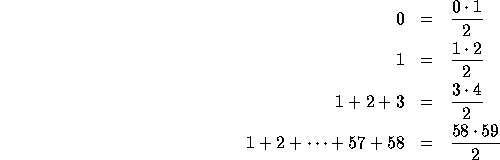
Each of these equations is easy enough to prove on its own, but it would seem that proving infinitely many equations takes infinitely many proofs.
Induction is a technique for using just two short proofs to prove infinitely many facts. There are two key parts to an inductive proof:
Let's do an example. For the base case we choose a small value--say, 1. The proof is quite easy (the sequence of values from 1 to 1 consists of just the value 1):
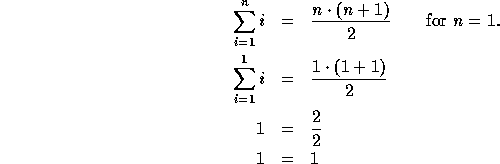
On the other hand, it would be quite tedious to prove
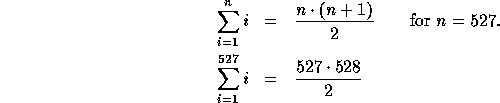
This would require quite a bit of math.
However, suppose that you were permitted to assume that
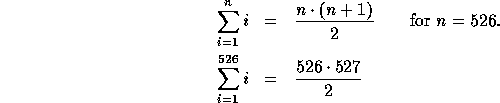
Then proving the property would be easy again:
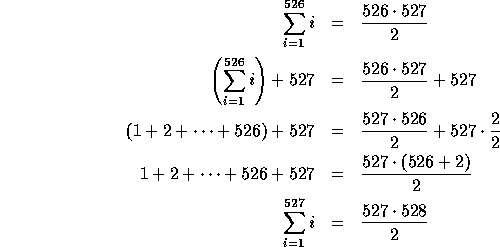
If we already have a proof that does most of the work for us, then extending that proof to demonstrate a new equation is not hard. We can generalize the above proof to show how, given a proof for arbitrary n, we can extend it to n+1:
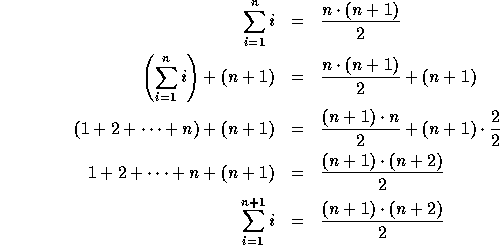
Now we have a new technique for proving the equations for any value of n: we start with the base case and repeatedly apply the inductive step until we have a proof for the desired value of n. For instance, to prove the equation for n=3, we start with the base case (n=1) and then apply the inductive step twice: once to demonstrate the equation for n=2, and once to extend it to n=3. Similaraly, the proof for n=527 consists of the base case plus 526 applications of the inductive step.
The inductive principle states that if we have a proof for the base case and a technique for extending a proof to the next logical step (in this case, extending a proof for one number to the next greater number), then we can construct a proof for any value at all. In other words, two small proofs--for the base case and the inductive step--were able to replace arbitrarily many proofs, one for each value of n. We have succeeded in proving our equation for every value of n.
After writing a program, you must verify that it is correct. (An incorrect program is in some ways worse than no program at all.) So far we have used testing to confirm that our programs operate correctly, but testing can only prove negative facts, not positive ones. That is, testing can demonstrate that a program is incorrect by giving an input for which the program gives the wrong answer, but testing cannot show that a program is correct for all inputs, because there might be some input for which the program fails (but which you forgot to test).
While testing produces facts about individual inputs, induction can make statements about groups of inputs, or about every possible input. Thus, induction is a technique for proving programs correct and providing complete confidence in your code, while testing can at best only provide partial confidence (unless you test your code on every possible input, which is generally an impossible task).
Induction is the natural counterpart to recursion: when you have created an arbitrarily-large object (or sequence of calls) via recursion, the best way to reason about it is via induction. The induction base case deals with the recursion base case, and the inductive step deals with the recursion.
Emacs supports a number of features that make editing and running C programs very convenient, so we will use the Emacs editor for the rest of the term. Many of you are already familiar with Emacs; here is some review that all of you might find helpful.
Start up Emacs by typing gnuemacs at your shell prompt or using the mouse to get the ``Comp 210 tools'' menu. Emacs is an editor, but it is also a richly-featured program development environment and much, much more. Many people, including the instructor for this course, do all their work from Emacs, including filesystem traversal, editing, reading and sending news and mail, debugging, surfing the Web, etc.
Emacs manages a collection of buffers, some of which are visible on the screen and some which may be hidden. A buffer is the object holding the text from a file or some other information, such as interaction with a program being run from Emacs. The blank line below the reverse-video status line is called the echo area (when Emacs uses it to display messages) or the the minibuffer (when you use it for specifying complex commands). Most Emacs commands have a long form starting with M-x and a short keystroke sequence (a keyboard accelerator). For instance, you can edit a file in its own buffer by doing any of
M-x is the meta-x keystroke, which you type by holding down the meta key (the diamond next to the space bar), pressing and releasing x, then letting up on the meta key. On some machines lacking a meta key, the alt key works as a meta key. If you don't have an alt key (or it doesn't work as a meta key), then you can type ESC x instead (press and release the escape key, then press and release x).
The universal quit command in Emacs is C-g; it almost always aborts the current command. Frequently, pressing ESC three times will also abort the current comment and/or quit the current mode.
Emacs is extensively documented; it is very easy to get help or to learn more about it. The keystroke C-h invokes help in Emacs; you follow it by another key to indicate what kind of help you want. To learn more about what sorts of things you can type after the first C-h, type a second one: C-h C-h. Some particularly useful help keystrokes are:
Of course, you can just use the pull-down menus if you prefer; most of Emacs's functionality is available from them. The place to start looking for help is on the "Help" menu.
The tutorial directory, ~comp210/Labs/lab10/, contains a copy
of the quick reference card for Emacs; it was also handed out in lab.
You might want to learn about multiple windows in Emacs, switching among windows and buffers, incremental searching, marking regions, the Dired directory editor, indenting C/C++ code, spell-checking, Emacs's command and filename completion facilities, and command shells within Emacs.
You are strongly encouraged to read the Extended C Primer that was handed out in class and is available on the WWW. It introduces you to the C language, and we will assume that you understand the material presented there. (So far you should have read up to, but not including, the section on arrays.)
Copy the contents of the lab directory by executing the following commands from a Unix shell:
cp -r ~comp210/Labs/lab10 ~/comp210 cd ~/comp210/lab10Use Emacs to view the file
simple.cc, which contains the
following text:
// An example program in Extended C
// Compile via g++ -Wall -g -o simple simple.cc
#include <iostream.h>
int Fact(int n)
{
if (n == 0)
return 1;
else
return n * Fact(n-1);
}
int main()
{
int n;
cout << "Enter a natural number ";
cin >> n;
cout << n << " factorial is " << Fact(n) << "\n";
}
If you run out of quota while compiling programs, use du to find out where space is being taken up. Likely possibilities include old executables and your Netscape cache.