
|
|
Comp210: Principles of Computing and Programming
|
So now, it's time to go
We've been working with lists all semester, but they've always been of a particular length. At some point, the empty list at the end is encountered and its all over. But not all lists are of a finite length. Take, for example, the list of all natural numbers, or all evens or all odds, or even more fun, say the list of all Fibonacci or prime numbers. How can we represent an infinite list in the computer?
But methinks thee practical side doth protest too much! "Not enough memory!" you cry.
Ahh, but we forget what a list is. Let's go back to day one:
A list is either
-- empty, or
-- non-empty, wherein it has a first and a rest, which is a list.
Yeah, yeah, yeah. We've heard it all before...
But did we actually hear what it said? Did it say that the list had a finite length? Did it say that the list had a length at all?
Hee, hee, hee... ;-)
Does our definition say how fast we should get an answer when we ask for the rest of a list?
Would anyone notice if we were just plain lazy and didn't bother to actually instantiate the rest, until after someone asked for it?
The process of delaying instantiations until they are needed is called lazy evaluation.
The opposite of lazy evaluation is "eager" evaluation.
Let's see how our LRStruct from Lecture 40 can be modified for lazy evaluation by considering these notions:
Bottom line: algorithms shouldn't be able to tell if a list is lazy or eager.
What does this all mean?
A mutable list must still be a LRStruct whether it is lazy or eager.
So how can we change the behavior of an LRStruct without changing its actual class, especially considering the fact that the list needs to dynamically change from lazy to eager?
Sounds like dynamic reclassification to me! ==> We need a new state!
But we don't want to rewrite what we already have. We already have a non-empty state that works just fine thank you. We just need to embellish it a bit to lazily evaluate rest.
That is, we want to simply intercept any calls that involve rest, instantiate a new rest, and then process the call normally.
This process of intercepting calls to do additional processing is called "decoration" and we will thus be describing the Decorator Design Pattern. The use of the Decorator design pattern to implement lazy evaluation in Java was first puublished in 2000 by Dr. Nguyen and Dr. Wong. This Scheme implementation is current research and has not yet been published. The process of delayed instantiation is also called "proxying".
The Decorator design pattern involves a "decorator" and a "decoree". The decoree is the original structure/class/object being used. Here the decoree is the non-empty state, NELRSState. The decoree provides the base functionality that we wish to augment. The decorator is a new structure/class that provides the new behaviors we wish to add. Here, the decorator is a new state we'll call "LazyLRSState" which will provide the lazy evaluation of rest. The decorator holds a reference to the decoree, so that the decorator only provides the new behaviors--when the original behaviors are needed, the decorator simply delegates the call to the decoree. More specifically, the decorator intercepts all the calls to the decoree, adding any additional behaviors it wants before and/or after it delegates the call to the decoree.
The key point is that the decorator is abstractly equivalent to the decoree. This enables the decorator to be used in place of the decoree without the user ("client") ever knowing it--ahh, the beauty of polymorphism! LRStruct can use a LazyLRSState just as easily as it uses the original two states. In fact, LRStruct never knows that it is lazy or eager!
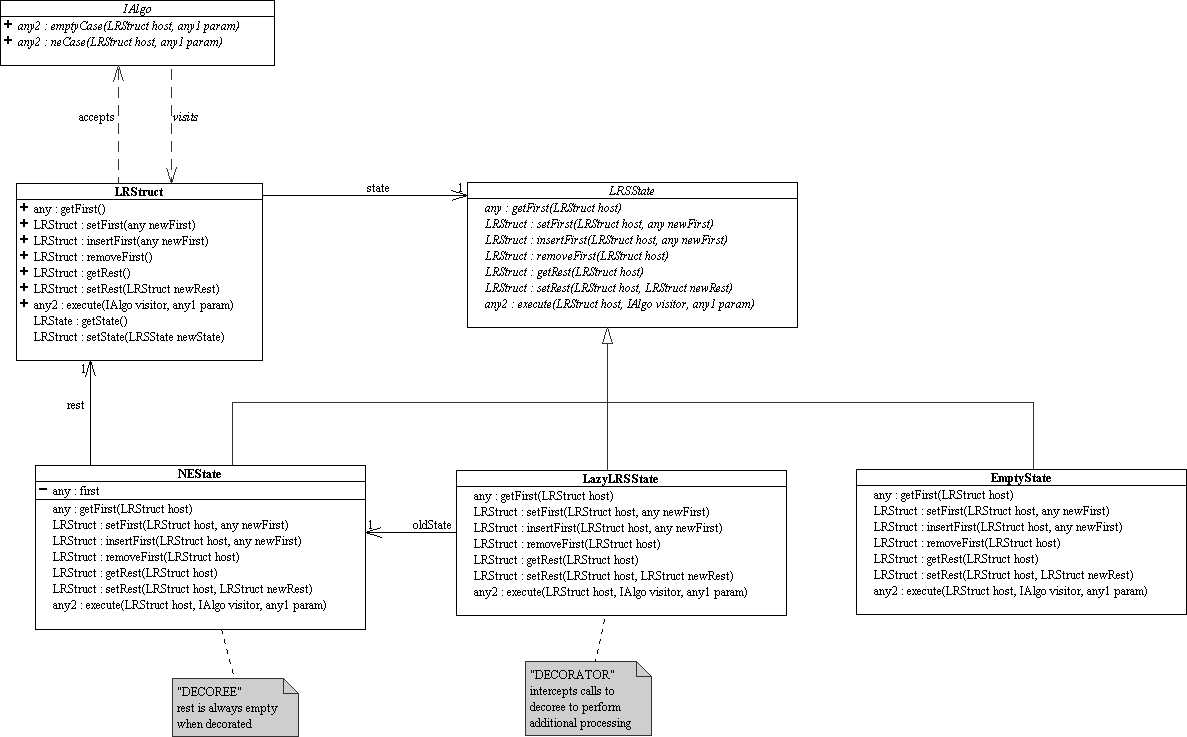
getFirst, setFirst, and execute don't involve rest, so LazyLRSState simply delegates these calls directly to oldState, its reference to the original NEState.
The other functions need more handling:
getRest: oldState has a rest which is an empty LRStruct. So LazyLRSState's getRest must generate a new rest and install it into oldState. A factory to generate a new lazy list is very useful here to generate the new rest. To return the LRStruct to an eager state, the LazyLRSState must remove itself from the system by setting its host's state to oldState.
setRest: This will eliminate the (current) laziness of the list because rest is being replaced with a supplied value. So setRest must first set oldState's rest to the new value and then set the host LRStruct's state to oldState.
insertFirst: This function must essentially replicate the behavior of NEState's insertFirst, with the difference that the state involved is the LazyLRSState rather than an NEState.
removeFirst: By delegating to its own getRest a new rest can be generated and installed into oldState. Then a delegation to oldState will process the removal of first. This is essentially the same as the original behavior but the guaranteed robustness provided by the delegating to getRest.
As noted above, a factory to instantiate lazy lists is very useful. This factory, which we'll call LazyLRSFactory, first instantiates a regular empty LRStruct and inserts an initial value. This creates an LRStruct with an NEState holding and EmptyState, which is what we want. Next, the factory simply instantiates a LazyLRSState, sets its oldState to reference the original NEState, and installs the LazyLRSState in its place in the LRStruct, which is then returned.
Now that seems simple enough, but there are two unanswered questions:
Question 2 is not unrelated to Question 1 in that if a factory is used to generate the new rest, then the factory will generate the needed first. But since the next value is not the same as the previous value, the factory must be different--or does it...?
The above description of the LazyLRSFactory is a description of its invariant behavior. The particulars of what values for first are generated are variant behaviors. Let's separate this variant behavior out from the invariant factory behavior.
We're working with a recursive process on a recursive data structure, so guess what, the variant behavior, which we'll encapsulate into a class called Generator, abreaks down into (drum roll please...)
Base case: generate a value for first.
Inductive case: generate the next Generator, which will generate the first the next time it is needed.
Thus a LazyLRSFactory needs to take a Generator as an input parameter and a LazyLRSState thus needs both a LazyLRSFactory and a Generator.
When getRest uses the LazyLRSFactory to generate the new rest, it hands the factory the next Generator produced by the current Generator.
;;A Generator is a structure which has
;; an initial value and an inductive function that
;; returns the next generator
;; first: any
;; next: --> Generator
(define-struct Generator (first next))
;; LazyLRSFactory: Generator --> LRStruct
;; Returns a lazy LRStruct which uses the supplied Generator to create the list.
(define (LazyLRSFactory aGen)
(local
[(define lrs ((LRStruct-insertFirst (LRSFactory)) (Generator-first aGen)))
(define lazyLRSState
(local
[(define oldState ((LRStruct-getState lrs)))] ;; decoree
(make-LRSState
(lambda (host) ;; getFirst
((LRSState-getFirst oldState) host)) ;; delegate to decoree
(lambda (host newFirst) ;; setFirst
((LRState-setFirst oldState) host newFirst)) ;; delegate to decoree
(lambda (host newFirst) ;; insertFirst
(begin ;; replicate normal behavior but with this state
((LRStruct-setState host) ((LRStruct-getState ((LRStruct-insertFirst ((LRStruct-setState (LRSFactory)) lazyLRSState) newFirst)))))
host))
(lambda (host) ;; removeFirst
(begin ;; replicates normal behavior but more robustly
((LRStruct-setState host)((LRStruct-getState ((LRStruct-getRest host)))))
host))
(lambda (host) ;; getRest
(begin
((LRStruct-setState host) oldState) ;; make eager
((LRStruct-setRest host) (LazyLRSFactory ((Generator-next aGen)))) ;; install new rest
((LRStruct-getRest host)))) ;; get the new rest
(lambda (host newRest) ;; setRest
(begin
((LRStruct-setState host) oldState) ;; make eager
((LRStruct-setRest host) newRest))) ;; delegate the call
(lambda (host visitor param) ;; execute
((LRSState-execute oldState) host visitor param)))))] ;; delegate to decoree.
(begin
((LRStruct-setState lrs) lazyLRSState) ;; install the lazy state.
lrs)))
Since a Generator is required to recursively generate itself, many implementations will hold an internal factory. Here's some examples of Generators:
;; Generator for natural numbers
(define natNumGen
(local
[(;; genFac: natNum --> Generator
;; x is the initial value to use.
define (genFac x)
(make-Generator
x ;; first: the initial value
(lambda () ;; next: next first is x+1
(genFac (add1 x)))))]
(genFac 0))) ;; start off first at zero
;; Here's an infinite list of all the natural numbers
(define natNums (LazyLRSFactory natNumGen))
;; Generator for odd natural numbers
(define oddNumGen
(local
[;; genFac: natNum --> Generator
;; x is the initial value to use.
;; returns a Generator for every other natural number,
;; starting at x
(define (genFac x)
(make-Generator
x ;; first: initial value
(lambda () ;; next: next first is x+2
(genFac (+ 2 x)))))]
(genFac 1))) ;; start off at 1 for odd numbers
;; Here's an infinite list of all the odd natural numbers
(define odds (LazyLRSFactory oddNumGen))
;; Generator for Fibonacci numbers
(define fibonacciGen
(local
[;; genFac: natNum natNum --> Generator
;; x1 is the previous Fibonacci number.
;; x2 is the initial Fibonacci number to use.
;; returns a Generator for the Fibonacci series,
(define (genFac x1 x2)
(make-Generator
x2 ;; first: initial value
(lambda () ;; next Fibonnaci number is x1 + x2
(genFac x2 (+ x1 x2)))))]
(genFac 0 1))) ;; start at 1
;; Here's an infinite list of all the positive Fibonacci numbers
(define fibs (LazyLRSFactory fibonacciGen))
;;---------------------------------------------------------------------------------
;;To create a lazy list of prime numbers, we need to create factories for generators:
;; natNumGenFac: natNum --> Generator
;; Factory for a generator for natural numbers
;; starting at x
(define (natNumGenFac x)
(make-Generator
x ;; first: the initial value
(lambda () ;; next: next first is x+1
(natNumGenFac (add1 x)))))
;; filterMultsGenFac: natNum LRStruct --> Generator
;; Generator for filtered numbers
;; Used to generate a lazy list where all multiples of x are
;; removed from loi
(define filterMultsGenFac
(local
[;; remFirstMults: visitor to an LRStruct to remove all the leading multiples of x from
;; the host.
;; emptyCase: LRStruct natNum --> empty LRStruct
;; neCase: LRStruct natNum --> LRStruct
;; Returns a list with all leading multiples of x removed
(define remFirstMults
(make-IAlgo
(lambda (host x)
empty)
(lambda (host x)
(if (zero? (modulo ((LRStruct-getFirst host)) x))
((LRStruct-execute ((LRStruct-removeFirst host))) remFirstMults x)
host))))]
(lambda (x loi)
(local
[(define newLOI ((LRStruct-execute loi) remFirstMults x))]
(make-Generator
((LRStruct-getFirst newLOI))
(lambda ()
(filterMultsGenFac x ((LRStruct-removeFirst newLOI)))))))))
(define no3s (LazyLRSFactory (filterMultsGenFac 3 (LazyLRSFactory (natNumGenFac 1)))))
"First 10 elements of no3s"
((LRStruct-execute no3s)LRS->listN 10)
;; Generator for prime numbers
(define primeGen
(local
[;; genFac: natNum list-of-integers--> Generator
;; p is a prime number.
;; returns a Generator for the prime series,
(define (genFac loi)
(local
[(define p ((LRStruct-getFirst loi)))]
(make-Generator
p
(lambda () ;; next prime number
(genFac (LazyLRSFactory (filterMultsGenFac p ((LRStruct-removeFirst loi)))))))))]
(genFac (LazyLRSFactory (natNumGenFac 2))))) ;; start at list of all integers >=2
;; Here's an infinite list all prime numbers
(define primes (LazyLRSFactory primeGen))
Download the code here (12/03/2003: Now includes the above prime number generator!) : lrstruct_lazy.scm (Be sure to set the language level to "Pretty Big").
Remember, all visitors (algorithms) are
completely independent of whether or not the LRStruct host is lazy or
eager!
(Though some may run for a long, long time and/or run out of memory if the
eager part of the list gets too large)
Last Revised Wednesday, 01-Dec-2004 09:52:44 CST
©2004 Stephen Wong and Dung Nguyen