Comp210: Principles of Computing and Programming
Fall 2004 -- Homework #9   

All problems will require all (applicable) steps from the design recipe, including a template. Before you tackle the homework, remind yourself of our General Advice, Advice on Homeworks (in particular: staple and provide questions), and the Grading Guidelines.

All problems require suitable test cases that cover the most important issues in a function's domain space!

Remember: Contract, purpose, header and test cases are always required!

For visitors, you need the following documentation:

1. Contract for the base case and inductive case functions -- since the contracts are the same between visitors, you only need to specify the contract in the define-struct for the visitor itself
2. A puirpose statement for the whole visitor -- what does the visitor do abstractly to its host?
3. Purposes for both the base case and inductive case functions -- you need two here, because the two cases do different things.

Be sure to load the teachpack draw.ss!

In this homework we will be exporing a new type of fractal: Tree Fractals.

A TreeFractal starts as a single Line:

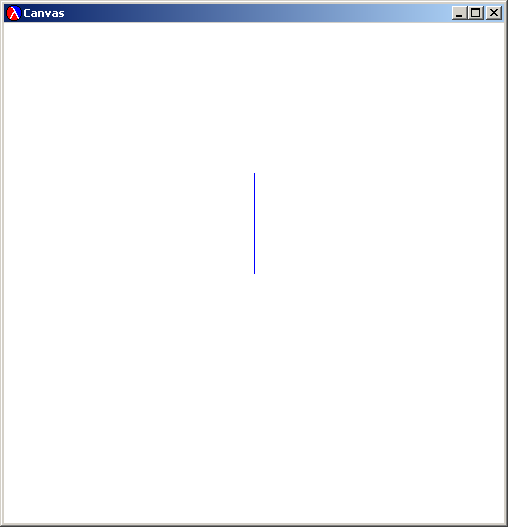
That Line is transformed into a Branch, which is the original Line, plus (in this case, 3) Lines "growing" from its endpoint:

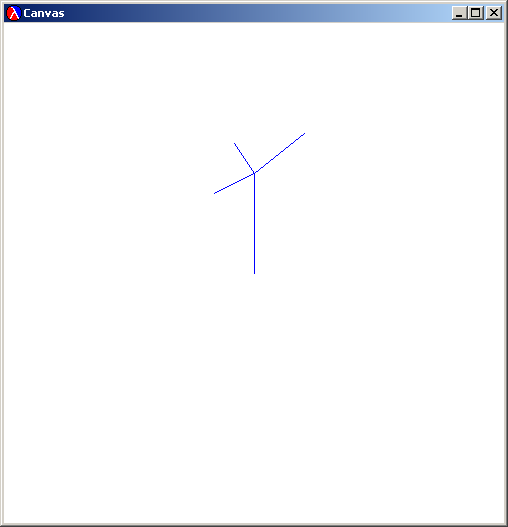
These new Lines are sized and are pointing relative to the original Line. We see that clearly if we go another iteration:

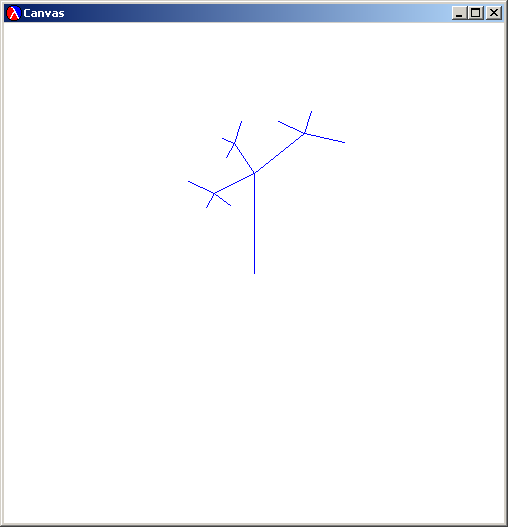
The process simulates the way a plant grows. After 8 iterations, we see a distinctly organic shape forming:

Changing the way a Branch grows from a Line changes the way the TreeFractal looks:

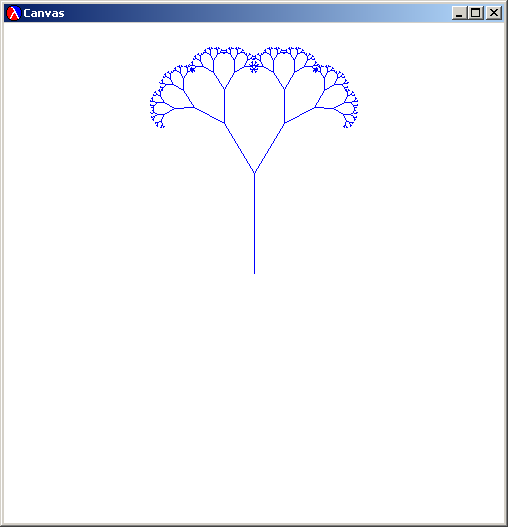
We can clearly see that

;;A TreeFractal is either

;;-- a Line 

;;-- a Branch





;;A Line is a struct of two points (posn)

;;(make-Line posn posn)

(define-struct Line (p1 p2))





;;A Branch is a Line plus a list-of-TreeFractals



;; (make-Branch Line list-of-TreeFractal)

(define-struct Branch (line loTF))





;;A list-of-TreeFractal

;; -- empty, or

;; -- (cons [TreeFractal] [list-of-TreeFractal])

The key to TreeFractals is defining a "prototype", which is the pattern of Lines added to the end of a given Line when it "grows" into a Branch. The problem is that the original Line may be of any length, start from anywhere, and pointed in any direction. Mathematically, what we want to do is to define a prototype branching with respect to a well-defined "unit" Line. That is, we define the branches we want with respect to an original Line that is 1 unit tall and originates at the origin, and points in the positive y-direction, i.e. (0, 0)--> (0, 1).

Since the prototype lines have one end at the origin, we only need to specify their end-points. For instance, the above TreeFractals used the following prototype lists of points respectively;

(list (make-posn .5 .4) (make-posn -.2 .3) (make-posn -.4 -.2))

(list (make-posn .3 .5) (make-posn -.3 .5) )

Note that the prototype lines are less than 1 unit in length, otherwise the fractal would grow in size indefinitely. Why?

But in order to grow a Line into a Branch, the prototype lines must be scaled to the relative size of any given Line, rotated so that they point in the correct relative direction, and then translated to sit at the end of the given Line. This means that the transformation of the prototypes for each Line at the ends of the TreeFractal are different. This is a perfect place to use a factory that takes in the original Line and produces a transformation based on that Line. For the mathematically oriented, this transformation is called an "Affine Transformation" and no, you don't need to know its details:

;; make-xform: Line --> (posn --> Line)

;; creates a transformation that will translate a point referenced to (0, 1) 

;; into the coordinate system defined by the given line as the unit length 

;; along the y-axis.

;; The lambda takes in a point and returns a line that starts at the end of the 

;; given line.

(define (make-xform line)

  (local

      [(define p1x (posn-x (Line-p1 line)))

       (define p1y (posn-y (Line-p1 line)))

       (define p2x (posn-x (Line-p2 line)))

       (define p2y (posn-y (Line-p2 line)))

       (define dy (- p2y p1y))

       (define dx (- p2x p1x))]

    (lambda (p)

      (local 

          [(define x (posn-x p))

           (define y (posn-y p))]

        (make-Line

         (Line-p2 line)

         (make-posn 

          (+ p2x (+ (* dy x) (* dx y)))  

          (+ p2y (- (* dy y) (* dx x)))))))))



 

To use this factory, simply map its result (given the original line) over the list of prototype points (refBranches below):

(define branchRefs (list (make-posn .3 .5) (make-posn -.3 .5) ))

(map (make-xform line) refBranches))

There are a few housekeeping issues:

• Since computer screen canvases have their origins at the upper left hand corner of the screen and have the positive y-axis pointing down, one needs to tranform from "graph" (normal mathematical) coordinates to "screen" coordinates.
• Likewise we would like the origin to be in the center of the canvas, not over at one corner.

  We can define up some utilities:

  ;; defines the width and height of the canvas
  
  (define width 500)
  
  
  
  
  
  ;; defines the point at the center of the canvas
  
  (define center (make-posn (/ width 2) (/ width 2)))
  
  
  
  
  
  ;; toScreen:  posn --> posn
  
  ;; translates a point in graph (mathematical)coordinates into a 
  
  ;; point in the screen (how the points map to the actual screen) coordinates
  
  ;; where the origin is at the center of the canvas and positive y direction is 
  
  ;; vertically up, not down.
  
  (define (toScreen p)
  
    (make-posn (+ (/ width 2) (posn-x p)) (+ (/ width 2) (- (posn-y p)))))
  
  
  
  ;; drawLine: Line color --> boolean
  
  ;; draws a line in given in graph coordinates
  
  ;; returns true if succesful
  
  (define (drawLine l color)
  
    (draw-solid-line (toScreen (Line-p1 l)) (toScreen (Line-p2 l)) color))
  
  
  
  ;; Opens up a new square canvas of size width
  
  (start width width)

With these utilities we don't have to worry about the screen at all and all of our drawings will come out as we expect, with the origin at the center of the canvas and the positive y-axis pointing upward.

The above code can be downloaded here: hw09.scm

Ok, we're finally ready to get started! The key here is to take things slowly and methodically. Remember, write small units -- test small units. Do NOT attempt to write the whole program at once!!

1. (25 pts total) Getting started
   1. Create a Line object and make sure that drawLine will draw it on the screen. A nice starting line is ((0,0) (0, 100))
   2. (15 pts) Write a function called "nextBranch" that takes a Line and a list of prototype points and returns a Branch. Remember that a Braanch contains the original Line plus a list of transformed prototype points. Use the make-xform function above.
   3. (10 pts) Write a function called "drawBranch" that draws a Branch whose list-of-TreeFractals holds only Lines at the moment (as in the output of nextBranch). drawBranch should take a Branch and a color as inputs. Remember to draw the Line contained within the Branch plus the list of Lines (TreeFractals) it contains. Hint: Use both "and" & "andmap". Do not manually recur over the list! (why?) Do you remember how we mapped functions of more than one variable?
      
      
2. (40 pts total) Now it's time to get some visitors.
   1. (10 pts) First we must write the invariant code: the visitor structure for a FractalTree called "TFVisitor" and the execute method, called "tfExecute".
   2. (15 pts) Write a TFVisitor called "drawTF" that will draw a FractalTree. The visitor's parameter should be the color of the tree. Use the base and inductive case solutions we developed in Prob. #1, substituting a real recursive call for the drawLine call in the inductive case. Remember that you don't know what is in the list-of-TreeFractal, so all you can do is to execute a visitor to process its elements.
   3. Be sure that you throughly test your program at this stage, using both Lines and the simple 1'st level Branch we made in Prob. #1.
   4. (15 pts) Write a TFVisitor called "growTF" that will take a TreeFractal and grow it one more level. Pattern your code after the drawTF, except that you are making Branches, not drawing. Modify the results of Prob. #1 to fit in a visitor. The visitor's parameter is a list of prototype points.
   5. Use growTF to manually create a tree of many levels. Test your drawTF with its output to make sure that it works.
      
      
3. (25 pts) Now for more levels
   1. (10 pts) To automatically create an n-level TreeFractal, we turn towards Natural Recursion. Write the execute ("nExecute") and the visitor (NVisitor) for Natural Numbers.
   2. (15 pts) Write an NVisitor called growNTF that will generate an n'th level TreeFractal. Here's what each case needs to do:
      1. Zero case: Return a new Line (the original starting line from above).
      2. Non-Zero case: Use your TFVisitor growTF from above to grow the result of the recursive call to growNTF.
         
         The parameter to growNTF is a list of prototype points.
         
         
   3. You should now be able to make a tree of arbitrary depth. Note that any depth over 10 is going to take a long time to calculate. Try different lists of prototype points too.
      
      
4. (20 pts) Pushing the envelope:
   1. (10 pts) Write a factory function called "make-nextBranch" that takes in a list of prototype points and returns a function that will take Line and return a Branch (compare this with nextBranch from above).
   2. (10 pts) Rewrite growTF and growNTF as growTF2 and growNTF2 so that they take the output of make-nextBranch instead of a list of prototype points. What have you accomplished by doing this? How have you further decoupled your TreeFractal code from what sort of tree it is actually making?
      

Step back for a moment and admire how such small chunks of simple code that are decoupled from each other can generate such complex output. This is the power of abstraction and is the heart of object-oriented and functional programming. This style of programming is arguably more object-oriented than functional, though in a true object-oriented language, there is one more powerful abstraction tool ("polymorphism" if you care) that really opens up the doors of abstraction.

We'll stop here, but it should bother you that the base case Line is hard-coded into our system. Also, the way the code is tied to the Branch being defined as having the original line in it should strike you as problematic. So, for 20 extra credit points, can you figure out a way to push the abstraction of our code up another notch?

Here's another extra credit problem for 15 points: Using foldr, write a factory function called "make-multiNextBranch" that takes in a list of list of prototype points and returns a function that will take a Line and return a Branch. Compare this with Prob. 4b above. This factory should take the original line and successively grow it once with each of the supplied lists of prototype points, returning the end result Branch. Show that without disturbing any other existing code, you can now create a TreeFractal that repeats an arbitrary series of different branching growths. Now that's power!

110 pts total + 35 extra credit.

Last Revised Sunday, 24-Oct-2004 17:02:04 CDT

©2004 Stephen Wong and Dung Nguyen