COMP 210, Spring 2001
Homework 7 : Map, fold, curry
Due Oct.17 (wed), at start of class; will also be accepted 19th (fri) at start of class.

You are NOT required to show the template for your programs (woo-hoo!). Your functions should still follow the template, though. And of course, each function should still have a contract and purpose, and reasonable test cases.

Before you tackle the homework, remind yourself of our General Advice, Advice on Homeworks (in particular: staple and provide questions), and the Grading Guidelines.

• posns,
• translate-shape: shape, num, num --> shape (hw02),
• draw-shape: shape --> true (hw02),
• draw-shapes: list-of-shape --> true (hw04),
• circle-tool : number --> circle (hw04; given a number, create a circle at 150,150 and radius proportional to the number),
• as well as some shapes named circ1: circle and rect1: rectangle.

1. (4pts) Write the following using map and foldr (but no explicit recursion):

   1. make-circles : list-of-number --> list-of-shape, which makes a circle out of every number in the input list, using the teachpack's circle-tool.
   2. translate-shapes : list-of-shape, posn --> list-of-shape. Translate each element of the list by the specified amount.
   3. max-list, which takes in a list and returns the largest element.
      Note: rather than say this function only takes in non-empty lists, we'll allow empty lists, and use negative infinity (#i-inf.0) as the sentinel value for empty lists.
      (This is a convenient value for max-list's code, but may or may not be a reasonable answer for different problems: If you are looking for the wealth of the richest person named Rumpelstilzkin, and you get the answer "infinitely in debt", does this mean there is no such name person, or were there so-named people who lost a wager to the tune of "more money than anybody can ever name"?)
   4. dot-product, which takes in two lists of n numbers ( a₁ a₂ ... a_n) and (b₁ b₂ ... b_n) and returns a₁* b₁ + a₂* b₂ + a_n* b_n (for any n >= 0). (What are some trivial test cases?)
      Hint: the built-in map actually can take in binary functions and two lists of arguments, as you wrote separately in the previous hw's map2.

2. (4pts)

   1. Write slope@, which takes in a function f : real --> real, a number x, and a positive number e (the "tolerance", usually small ... whatever "small" means). It returns an approximation to the slope of f at the point x, according to the math formula:

      slope@(f,x,e) = (f(x+e) - f(x-e)) / 2e
      

      (Thus, the slope of a horizontal line (constant function) is 0 everywhere, and of a line at 45 degrees (identity function) is 1 everywhere, and a curve which is horizontal "for a moment" has a slope of 0 just at that point (e.g. the top of the St. Louis arch).)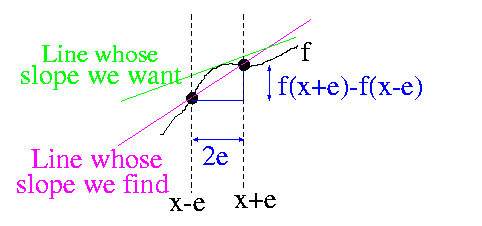 Aside: Really, we're precisely computing f's average slope, between x-e and x+e (provided f is continuous) The hope is, the function's slope at a particular point is close to its average nearby slope (where "nearby" means "within e"). A good bet for most functions, but the wigglier f is, the worse our guess is (for a fixed e); a few functions wiggle wildly (like lambda x . sin(1/x) near 0).
      To think about: How might you decide whether a function is very wiggly, so that your function might automatically decide to try a smaller e?
      This problem does not require any knowledge of calculus -- only the math mentioned here. If you have had calculus: What is the diference between this approach of finding the derivative, vs the approach taken by programs like Mathematica? (Which is closer to what you spent months learning, in calculus?)
      Also, why does the above formula compute precisely the average slope of f between two points (if f continuous)? The average of a function between a and b, is the integral from a to b divided (normalized) by (b-a); Note that the integral of f' from a to b is f(b)-f(a) -- that's the fundamental theorem of calculus!: We can determine the average value of f' over an entire interval, only by knowing f at the endpoints.)

   2. We'll make a curried version of this: Write the function slope, which takes in a function f : real --> real, and returns a function real --> real, which takes in any point and returns (an approximation of) the slope of f at that point.
      (You may instead call this derivative or d/dx if you like.)

3. (4pts) Consider the idea of iterating a function: for instance, if I repeatedly double 3, I get 6, then 12, then 24, etc. That is, I take the output of a function, and again apply the function to that.

   Iterating square twice, starting with 5, yields (square (square 5)) = 625. If I had a function remove-max: list --> list, then iterating that three times starting with (list 7 18 2 9 3) means

   (remove-max (remove-max (remove-max (list 7 18 2 9 3))))
   =
   (list 2 3)
   

   In general, iterating some function f 3 times starting with i means (f (f (f i))).

   1. Write the function iterate, which takes a function, a natNum, and an initial input to the function, and iterates the function that many times. (e.g. we saw (iterate remove-max 3 (list 7 18 2 9 3)). (Hint: what template will you base your code on?)

   2. Extra credit (1pt): Write two different versions of iterate, one which is tail-recursive and one which isn't (and indicate which is which, of course).

   3. Using iterate, write remove-first-n, which takes a number n and list, and returns the list with the first n items removed. (Of course, an error would result if the list had fewer than n items.)

4. (extra credit: 2pts) Be sure to include contracts:
   1. Write the function curry, which takes in any binary function and returns a curried version of it. (For instance, (curry +) returns a function equivalent to the lecture note's make-adder.)
   2. Write the inverse function, uncurry, which takes in a curried function of one argument, and returns a two-argument function.
   3. Now write curry3to2, which takes in ternary functions and returns binary functions (expecting the first two of the three original arguments). Use this to write a curried version of foldr, and define a couple of list functions (e.g. sum, map) using this curried foldr.