Newton's Law of Viscosity: Appendix B.1
We can now attempt to use the definitions that we have to write Newton's Law of Viscosity
![]()
In Maple, given our previous definitions this can be written as follows. First, since we will need the Transpose function, we implement the LinearAlgebra package.
| > |
Next, note that the following code gives a 3x3 matrix of ones.
| > |
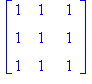
Now we simply write Newton's Law of Viscosity in Maple code.
| > |

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
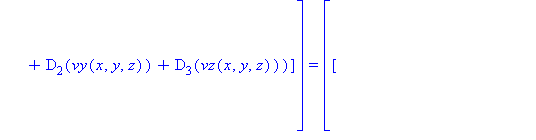
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

The result is a mess and simplification does not help, as seen below.
| > |

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
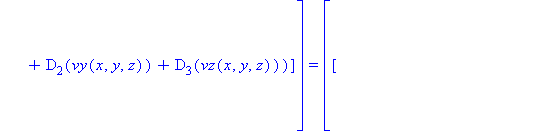
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
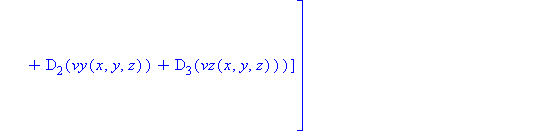
Note at this point, it will still be necessary to redefine the Jacobian as we did with the divergence. If this is not done, evaluation at a specific x, y, and z could result in problems. Furthermore, we can see that the given equation is still not completely functional for solving as general system of equations.