Constructing a Tensor Versus Constructing a Matrix 

When creating a tensor, it is first important to understand the various subscripts.  For instance, in the following equations, would signify x-momentum moving in the y direction.  The second thing that we need to do is to implement Maple's tensor package. 

>

 

Warning, the previous binding of the name Jacobian has been removed and it now has an assigned value 

We will now create the general Tensor its components are completely general functions of x, y and z at this point.  The function create is used to do this.  The first array [-1,-1] which is passed to the function create specifies the covariant or contravariant nature of each index of the tensor.  You can read more about this by typing in Maple's command line.  The second array which is passed to create is an array consisting of each row that should be stored in the tensor, with each row being separated by comma. 

>

 

To get a better idea of what τ actually looks like we can simply type the new tensor's name in the command line as follows. 

>

 

We could also create a matrix, which owing to its similarity to a tensor may actually prove more useful in a given application. 

>

 

To get a better idea of what τMatrix looks like we can simply type its name in the command line. 

>

 

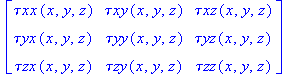
As you can see, this looks more like what we would expect to see.  In fact, Maple's built in functions seem to work more easily with matrices than with tensors.