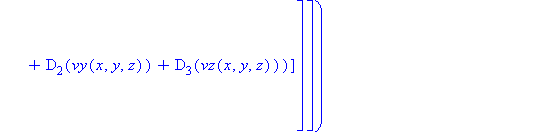An Application from Appendix B.1
Although some operations do not seem to be predefined in Maple, the necessary operations do work as expected, we can now use Appendix B.1 of Bird, Stewart, and Lightfoot to define the individual components of τ as functions of x, y, and z. However, before I do so, I note that the use of tensors is not compatible with the use of the divergence operator ∇. instead, we use our own function Divergence2 to accomplish the divergence operation.
| > | )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_1.gif){kind=small} )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_2.gif){kind=small} |
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_3.gif){kind=small}
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_4.gif){kind=small}
| > | )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_5.gif){kind=small} )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_6.gif){kind=small} |
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_7.gif){kind=small}
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_8.gif){kind=small}
| > | )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_9.gif){kind=small} )(x, y, z)+(2/3*mu-kappa)*Divergence2(v(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_10.gif){kind=small} |
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_11.gif){kind=small}
)(x, y, z)+(2/3*mu-kappa)*(D[1](vx(x, y, z))+D[2](vy(x, y, z))+D[3](vz(x, y, z))) end proc], [proc (x, y...](images/An Application from Appendix B.1_12.gif){kind=small}
| > | )(x, y, z)+(D[2](vx))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_13.gif){kind=small} |
)(x, y, z)+(D[2](vx))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[1](vy))(x, y,...](images/An Application from Appendix B.1_14.gif){kind=small}
| > | )(x, y, z)+(D[2](vx))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_15.gif){kind=small} |
)(x, y, z)+(D[2](vx))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[1](vy))(x, y,...](images/An Application from Appendix B.1_16.gif){kind=small}
| > | )(x, y, z)+(D[3](vy))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_17.gif){kind=small} |
)(x, y, z)+(D[3](vy))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[2](vz))(x, y,...](images/An Application from Appendix B.1_18.gif){kind=small}
| > | )(x, y, z)+(D[3](vy))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_19.gif){kind=small} |
)(x, y, z)+(D[3](vy))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[2](vz))(x, y,...](images/An Application from Appendix B.1_20.gif){kind=small}
| > | )(x, y, z)+(D[3](vx))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_21.gif){kind=small} |
)(x, y, z)+(D[3](vx))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[1](vz))(x, y,...](images/An Application from Appendix B.1_22.gif){kind=small}
| > | )(x, y, z)+(D[3](vx))(x, y, z)), x, y, z); 1](images/An Application from Appendix B.1_23.gif){kind=small} |
)(x, y, z)+(D[3](vx))(x, y, z)) end proc], [proc (x, y, z) options operator, arrow; -mu*((D[1](vz))(x, y,...](images/An Application from Appendix B.1_24.gif){kind=small}
We can now see that τMatrix is effectively a function of x, y, and z. Note if needed the function eval can be used to display a tensor or matrix, although in many cases it is unnecessary.
| > |  |
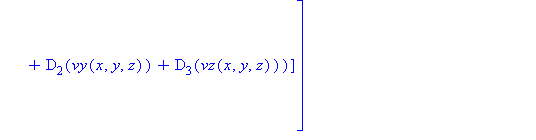
At least as far as the definitions in Appendix B.1 are concerned, τ also appears to posses the desired properties to display as expected.
| > |  |
