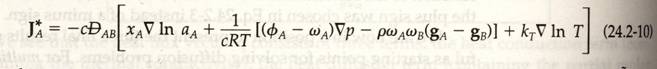Governing Equations

The most relevant equations needed to solve the problem boil down to variations of the generalized Stefan-Maxwell and Fick equations. These equations must, however, take into account the presence of external forces from electric current. Thus, the equations—almost identically transferred from editions 1 to 2—are listed here and explained.

Generalized Fick equations

The second edition text gives equation (24.2-3) as the relationship of multicomponent mass fluxes to the phenomelogical and transport coefficients. Phenomelogical coefficients are merely a species’ transport properties, and the sum over all species is zero. Here they are labeled as D^T for the substance α. These are also known as multicomponent thermal diffusion coefficients, and are neglected in the solution to problem 18.5-4. Of greater importance are the multicomponent Fick diffusivities, . The diffusivities are symmetric and the sum of the diffusivities multiplied by their mass fractions equals zero.

Similarly, edition one explained the Fick equations through the following method.

The total molar flux of the system would be a sum of average molar fluxes from each diffusion contribution:

Each diffusional flux, represented by the superscripts x, p, g and T for concentration, pressure, forced and thermal diffusion respectively, could then be more specifically defined based on the means of diffusion. For the problem in question, only concentration and forced diffusion were considered. The equations are as follows:

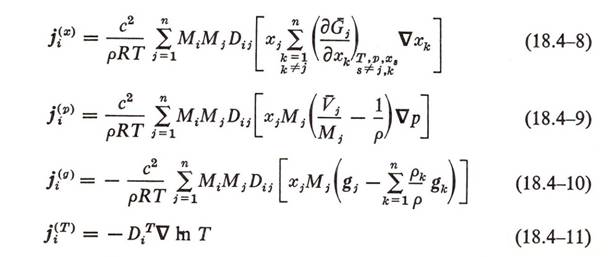
Similarly to the corollaries of (24.2-3), edition one submits that:

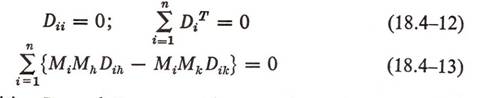
where M of i and h is the molar mean molecular weight. Ultimately, these relationships lead to the equivalent of (24.2-3) in the first edition:

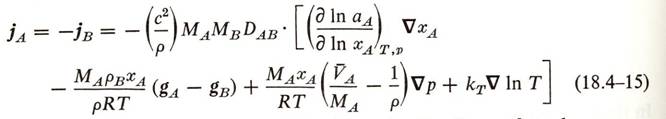
From these equations, the driving forces for each system may be determined.

Generalized Stefan-Maxwell Equations

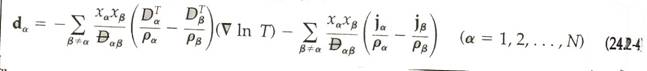
Equation (24.2-4) of the second edition text solves for d_α, the diffusional driving forces which account for the various diffusion modes, such as concentration, pressure and forced diffusion. Driving forces are defined such that their sum over all species α is zero. The attainment of this explicit formulation for the driving forces is given by solving for it in the Fick equation. For the problem herein solved, the forced diffusion driving force is provided by the electric current. Thus, d may be given as g in the following equation:

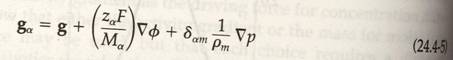
g without the subscript is the gravitational acceleration, z_α is the elementary charge on α, F is Faraday’s constant, Φ is the electrostatic potential, and the subscript m represents any mechanically restrained matrix, such as a permselective membrane. This last term was not used in solving the Maple problem.

The most typical diffusional form encountered in transport processes involves binary gas or liquid systems. In fact, though the example problem solved is a ternary system, the assumption that the ions in solution acted as a binary system with water is well-founded. Thus, the ruling equation for these circumstances was, as presented in the second edition: