Example 23.1-2: Binary Splitters

>

_____________________

Feed (F, z, Z) | | Product (P, y, Y)

--------------> | | ------------------>

| |

|________________|

|

|

V

Waste (W, x, X)

Streams Rate mol frac A Compounds

1 Feed F z 1 A (desired)

2 Product P y 2 B

3 Waste W x

> restart;

Ø eq23_1_13:= z*F = y*P + x*W; macroscopic mass balance for component A (eq. 23.1-13)

Ø W:= F - P; rearrangement of equation 23.1-14 (also mass balance)

> P:= theta*F; theta is the ratio of the molar rates of the product and the feed streams and is known as cut

After substituting these two equations into equation 23.1-13. we obtain

Ø z:= simplify(solve(eq23_1_13, z));

Ø zbook:= theta*y + (1-theta)*x; eq. 23.1-15

Ø simplify(z-zbook); our equation agrees with that of the book

Ø eq23_1_16:= Y = alpha*X; where alpha is the separation factor (characterizes the separation capability of the splitter)

Ø Y:= y/(1-y); X:= x/(1-x); equations 23.1-17,18

After combining equations 23.1-16,17,18, we can obtain an expression for y

Ø y:= simplify(solve(eq23_1_16,y));

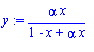
Ø ybook:= alpha*x/(1+(alpha-1)*x);

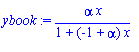
Ø simplify(y - ybook); we see that our y matches that in the book (eq. 23.1-19)

the same is true for x.

Ø y:= 'y';

Ø x:= simplify(solve(eq23_1_16,x));

Ø xbook:= y/(alpha - (alpha-1)*y);

Ø simplify(x - xbook); we see that our x matches that in the book (eq. 23.1-20)