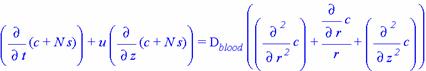Capillary Region Diffusion Equation

In the capillary region, whole blood flows with a velocity profile u(r). It's assumed here that the red cells travel with the same velocity as plasma at the same radial position. A "smoothing" assumption for diffusion through blood must be made, since blood is a heterogeneous fluid. The red cells occupy roughly half the volume of the blood. Within the red cells, hemoglobin reacts with gases such as oxygen and carbon monoxide, and diffusion occurs. However, the diffusivity in the concentrated hemoglobin solution within the red blood cells is different than the diffusivity within the plasma surrounding those cells.

A reasonable way to approximate the overall diffusivity is by using an analogy to the calculation of overall transfer coefficients for heat and mass transfer through a series of resistances (similar to the calculation of total resistance within an electric circuit), with the result

Using this, the equation found for diffusion in the tissue region becomes

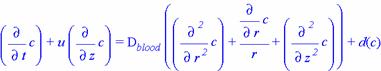
You'll note that the left-hand side is significantly different from the equation developed for the tissue region, namely that it has an extra term. This second term arises from the fact that, in a flowing system, the species flux along the axis would be

Assuming a constant cross-sectional area for the capillary, u is independent of z. The term

then gives, upon rearrangement, the convective term that appears in the diffusion equation.

However, this is only valid for a large capillary. In a small capillary, it is necessary to introduce two diffusivities; Dr=DHb for the radial diffusion process, and Dz=Dblood for the axial process. In this case, the diffusion equation would take the form

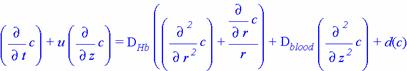
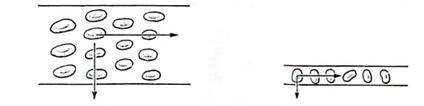
Notice in the above figure how in the large capillary, the radial direction vector contains both red blood cells and plasma, while in the small capillary, only a red blood cell (and a very small amount of plasma) is included in the diffusion route. This is why the two equations are necessary, but for simplicity’s sake I will only deal with the large capillary from here on out.

The term d(c) I've been using represents the generation of oxygen within the blood due to the dissociation of oxyhemoglobin (oxygen bound to hemoglobin). The equilibrium for the reaction depends upon the oxygen content of the plasma external to the red cell. Since the kinetics of this reaction are fast in comparison to diffusion rates, it is safe to assume that the fraction of oxygen bound to hemoglobin is always in equilibrium with respect to the oxygen content of the plasma. The fractional saturation, s, may be described as

where K is a constant dependent on the ionic strength and hemoglobin concentration of the plasma, and n fluctuates between 2.5 and 2.6. If we take N to be the oxygen-binding capacity of blood (moles hemoglobin/volume blood), then the generation of oxygen by dissociation is given by

Hence, the diffusion equation (for a large capillary) becomes