The Krogh Cylinder

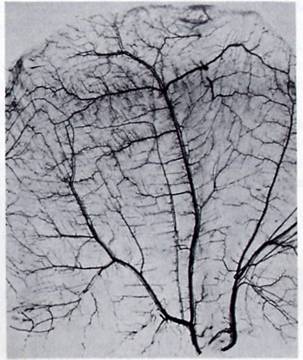
The above figure shows the vascular pattern typical of skeletal muscle in mammals. While not all tissue regions exhibit the geometrical regularity of skeletal muscle, it is still tempting to introduce the concept of a repetitive unit structure as a representation of the capillary-tissue region.

The Krogh cylinder, a concept introduced by Nobel Laureate August Krogh is shown below. This unit structure implies that each section of capillary is responsible for the supply to a corresponding cylindrical section of surrounding tissue.

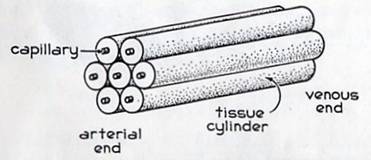
In order to yield a model amenable to solution, a few assumptions need to be made

- The Krogh cylinder is assumed to be an appropriate model for the geometry, even though some regions (such as in the neighborhood of branches) do not enjoy such geometrical simplicity

- The tissue surrounding the capillary is actually a heterogeneous composite of materials with metabolic chemical reactions taking place. In order to idealize this situation, we will assume that the chemical reactions are continuously, evenly distributed.

- Symmetry about the axis of capillary-tissue cylinder will be assumed. This “smoothing” aspect of the model suggest that there is a cylindrical surface about a capillary across which transport from surrounding capillaries just balances transport toward these capillaries. Hence, net transport rates vanish along this surface, which can be called a “no-flux” cylinder.

There are two transport regions of concern here. Within the capillary, material is transported through the blood by both convection and diffusion. If rc is the radius of the capillary, then a transport equation must be written for the material of interest over the cylindrical region 0<r<rc. Outside of the capillary, in the tissue, another transport equation must be written over the region rc <r<rt, where rt is the radius of the “no-flux” cylinder referred to previously.