Section 11.5 - Dimensional Analysis of the Equations of Change for Nonisothermal Systems

Use the standard equations of change (Eqns 11.5-1 to 3) to derive the dimensionless equations of change (Eqns 11.5-7 to 9) for the case of one spacial variable and time by using the dimensionless transformations outlined in the text (Eqns 11.5-4 to 6).

>

restart;

>	with(PDEtools,dchange):

The continuity equation in one spacial variable and time, Eqn 11.5-1

>	econt:=D[1](v)(x,t)=0;

>	tr1:={v(x,t)=vhat(xhat,that)*vo,x=xhat*lo,t=that*lo/vo}:

Changing variables in the differential equation produces the dimensionless continuity equation in one spacial variable and time, Eqn 11.5-7

>	Decont:=simplify(dchange(tr1,econt,[vhat(xhat,that),xhat,that])*lo/vo);

The equation of motion in one spacial variable and time, Eqn 11.5-2

>	emot:=rho*(D[2](v)(x,t)+v(x,t)*D[1](v)(x,t))=-D(P)(x)+mu*D[1,1](v)(x,t)-rho*gx*beta*(Temp(x,t)-Tempbar(x,t));

>	tr2:={v(x,t)=vhat(xhat,that)*vo,x=xhat*lo,t=that*lo/vo,P(x)=Phat(xhat)*rho*vo^2+Po,Temp(x,t)=Temphat(xhat,that)*(T1-T0)+T0,Tempbar(x,t)=Tempbarhat(xhat,that)*(T1-T0)+T0}:

Changing variables give the dimensionless equation of motion in one spacial variable and time.  It is clear that the left hand side is just the total derivative of the dimensionless velocity as is found on the left hand side of Eqn 11.5-8, but it is not clear whether the right hand side of this equation is in agreement with the right hand side of Eqn 11.5-8.

>	Demot:=simplify(dchange(tr2,emot,[vhat(xhat,that),xhat,that,Phat(xhat),Temphat(xhat,that),Tempbarhat(xhat,that)])*lo/rho/vo^2);

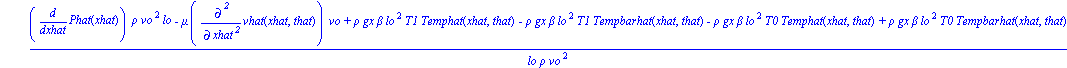
The right hand side of Eqn 11.5-8 is...

>	rhsBook:=convert(-D(Phat)(xhat)+mu/(lo*vo*rho)*D[1,1](vhat)(xhat,that)-gx*lo*beta*(T1-T0)/vo^2*(Temphat(xhat,that)-Tempbarhat(xhat,that)),diff);

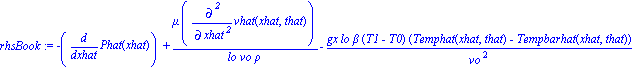
The right hand sides are in agreement and therefore our expression for the dimensionless equation of motion is equivalent to Eqn 11.5-8.

>	simplify(rhsBook-rhs(Demot));

The equation of energy in one spacial variable and time, Eqn 11.5-3

>	een:=rho*Cphat*(D[2](Temp)(x,t)+v(x,t)*D[1](Temp)(x,t))=k*D[1,1](Temp)(x,t)+mu*Phi(x);

>	tr3:={v(x,t)=vhat(xhat,that)*vo,x=xhat*lo,t=that*lo/vo,Temp(x,t)=Temphat(xhat,that)*(T1-T0)+T0,Phi(x)=Phihat(xhat)*(vo/lo)^2}:

Changing variables give the dimensionless equation of energy in one spacial variable and time.  Once again, it is clear that the left hand side is just the total derivative of the dimensionless temperature as is found on the left hand side of Eqn 11.5-9, but it is not clear whether the right hand side of this equation is in agreement with the right hand side of Eqn 11.5-9.

>	Deen:=simplify(dchange(tr3,een,[vhat(xhat,that),xhat,that,Temphat(xhat,that),Phihat(xhat)])*lo/vo/(T1-T0)/rho/Cphat);

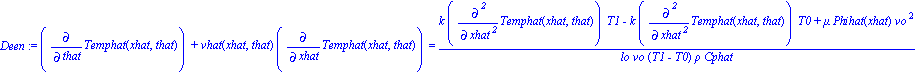
The right hand side of Eqn 11.5-9 is...

>	rhsBook:=convert((k/(lo*vo*rho*Cphat))*D[1,1](Temphat)(xhat,that)+(mu*vo/(lo*rho*Cphat*(T1-T0)))*Phihat(xhat),diff);

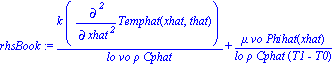
The right hand sides are in agreement and therefore our expression for the dimensionless equation of motion is equivalent to Eqn 11.5-9.

>	simplify(rhsBook-rhs(Deen));

Show how the dimensionless groups in Table 11.5-1 arise by making appropriate substitutions and assumptions.

The coefficients of each of the last two terms in the dimensionless equations of motion and energy (Eqns 11.5-8 & 9) form dimensionless groups.  Manipulation of these dimensionless groups, along with simplifications made when taking into consideration the relative magnitude of the forces involved, leads to simple expressions comprised of commonly used dimensionless groups such as the Reynolds, Prandtl, Brinkman, and Grashof numbers.  The dimensionless groups are listed in below and in Table 11.5-1 along with their simplified forms for each given case.

>

restart;

>	Group1:=vo->mu/(lo*vo*rho);

>	Group2:=vo->g*lo*beta*dT/vo^2;

>	Group3:=vo->k/(lo*vo*rho*Cphat);

>	Group4:=vo->mu*vo/(lo*rho*Cphat*dT);

Definitions of commonly occurring dimensionless groups:

>	mu:=lo*vo*rho/Reynolds: Reynolds number

>	beta:=Gr*nu^2/(g*dT*lo^3): Grashof number

>	k:=Cphat*mu/Pr: Prandtl number

>	dT:=mu*vo^2/(k*Br): Brinkman number

Definition of the kinematic viscosity and the thermal diffusivity:

>	nu:=mu/rho: Kinematic viscosity

>	alpha:=k/(rho*Cphat): Thermal diffusivity

Forced Convection Case:  Choose vo = vo.  Since inertial forces dominate buoyant forces in this case, Gr << Re^2.

>	Group1(vo);

>	Group2(vo);

In taking the limit of Group 2 as the Grashof number goes to zero, we find for the case of Forced Convection, in which inertial forces dominate buoyant forces, that this term should be neglected.

>	limit(Group2(vo),Gr=0);

>	Group3(vo);

>	Group4(vo);

Intermediate Case:  Choose vo = vo.  Relative magnitude of all dimensionless groups are similar, and therefore all dimensionless groups may be important.

>	Group1(vo);

>	Group2(vo);

>	Group3(vo);

>	Group4(vo);

Free Convection Case (A):  Choose vo = nu / lo.  Since heat transport by conduction dominates the heat produced by viscous dissipation for this case, the Brinkman number will be << 1 and therefore should be neglected.

>	Group1(nu/lo);

>	Group2(nu/lo);

>	Group3(nu/lo);

>	Group4(nu/lo);

In taking the limit of Group 4 as the Brinkman number goes to zero, we find for the case of Free Convection in which heat transport by convection is dominant, that this term should be neglected.

>	limit(Group4(nu/lo),Br=0);

Free Convection Case (B):  Choose vo = alpha / lo.  Heat transport by conduction dominates the heat produced by viscous dissipation in this case as well, thus the Brinkman number will be << 1 and therefore should be neglected.

>	Group1(alpha/lo);

>	Group2(alpha/lo);

>	Group3(nu/lo);

>	Group4(nu/lo);

In taking the limit of Group 4 as the Brinkman number goes to zero, we find for the case of Free Convection in which heat transport by convection is dominant, that this term should be neglected.

>	limit(Group4(nu/lo),Br=0);

Written by Seth Neumuller, April 14, 2004