Heat transfer through a composite medium.

Composite materials are widely used for purposes associated with chemical engineering. Many of these applications of composite materials involve the transfer of heat.  Therefore it is convenient to understand how develop expressions that model the heat transfer in composites.  This project illustrates the derivation of an equation to represent the transfer of heat though a very specific type of composite, but it serves as a model that with only slight modifications could be applied to any composite.

This composite material analyzed is made up of a solid matrix with particles implanted within it.  Much like a chocolate chip cookie.  Only not at tasty.  The matrix is assumed to have a uniform thermal conductivity, density and heat capacity.  The implanted particles are assumed to be spherical and have constant thermal conductivity, density and heat capacity.

The trick behind this derivation is to define a surface of contact conductance "m" This surface of contact conductance is what separates the spherical particles from the matrix.  A cross section of the composite material is shown below.

Having defined a surface of contact conductance, we can use Fourier's Law and model the normal component of heat flux across a contact surface to be proportional to the difference of temperature on both sides of the surface.  If we assume  that each particle is surrounded by the same uniform matix temperature (pretty good assumption for a chocolate chip cookie...and many composites used in engineering) the heat flux into each particle is in the radial direction with a magnitude of q_m=m(T_m-T_p(R)).

The derivation is as follows:

ASSUMPTIONS

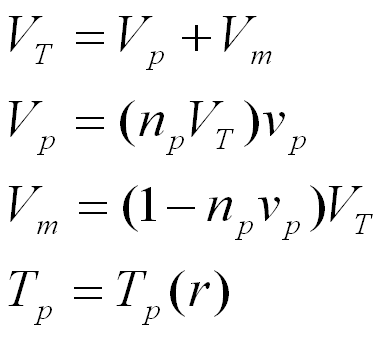
HEAT TRANSFER CONSTITUTIVE EQUATIONS

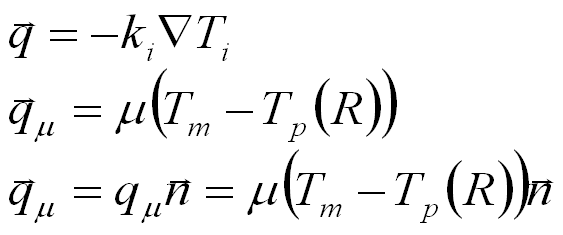
DERIVATION

Start with the general equation of energy (8) and simplify to obtain (9) which with further simplification leads to (10)

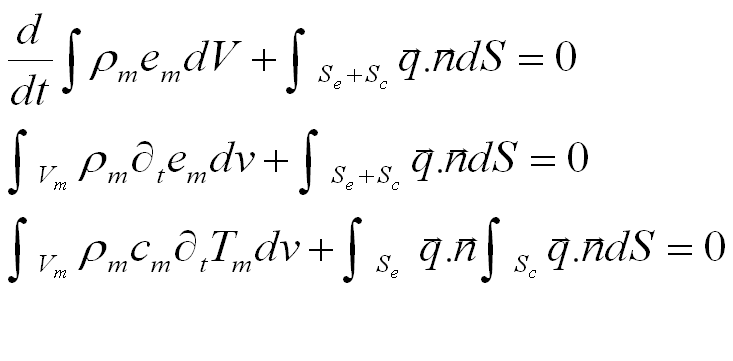
(Q is the heat energy per time entering any particle in the composite.  ap is the surface area of the sphere and qm is the heat flux int the particles of the composite.  We multiply Q by the total number of particles We find the total energy rate out of the matrix through contact conductance surfaces Sc (12)  We substitute this into (10) to find (13).  We define an element in catesian coordinates with dimensions delta x delta y delta z.  The surface integral in (13) is now represented by (14).  The integrals are evaluated as indicated in (15) .)

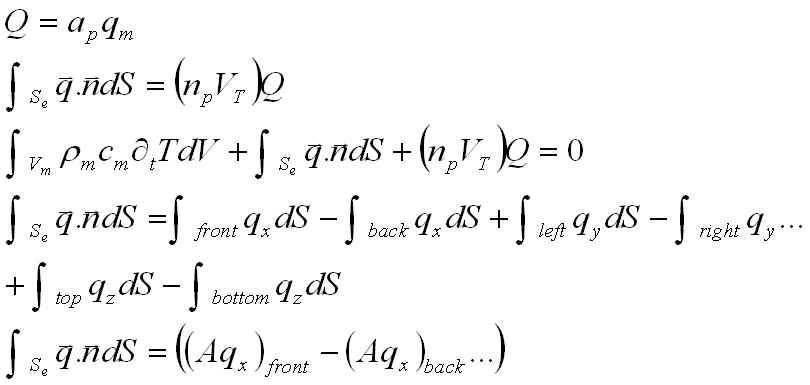
(To procede we must make the aproximation that if a plane intersects the composite the area of intersection between the matrix and the plane is equal to the fraction (1-npvp) of the total area of the composite.   Making this approximation leads to (16), rearranging we obtain (17) and (18) is the outcome of (17) after taking the limit of this expression as delta x, delta y and delta z go to infinity.  (19) is a more compact way of expressing (18)

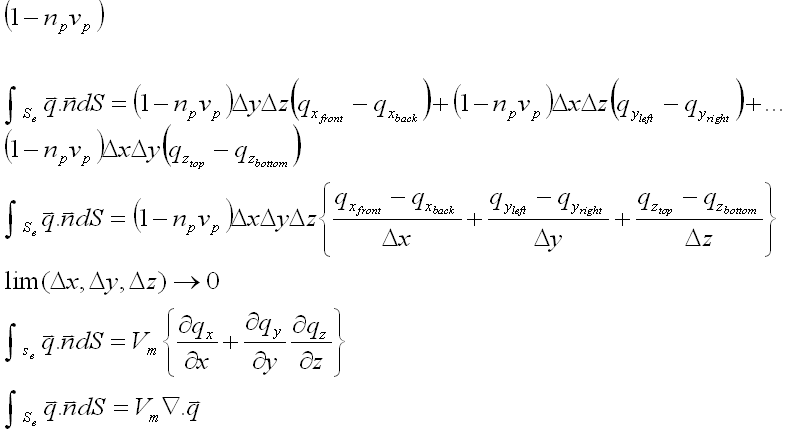
Substituting (19) and (11) into (13) we get (20).  Substituting (3) into (20) leads to (21).  Dividing by Vm and taking the limit of the expression as Vm goes to infinity we obtain (22).  The relationship between the area and the volume of a sphere is given by (23) Inputing this expression into (22) provides (24).  By using (5),(6),(7) we can simplify expression (24) into (25).  By letting  grouping all the constants, conductivity, density and heat capacity into one single constant defined as psi, we can further simplify the expression and get (26).  Substituting  (6) into (26) we finaly arrive to (27).

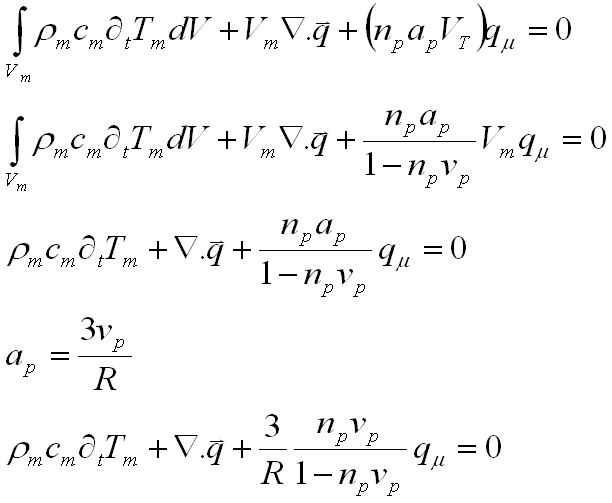
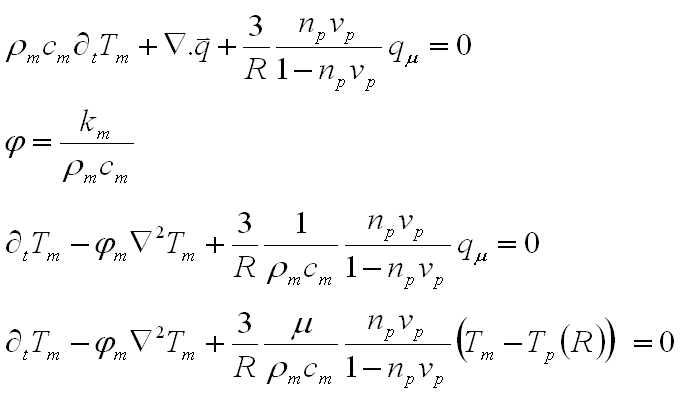
This last equation is defined as as the matrix thermal diffusivity. One can notice that this equation includes two variables Tp(R) and Tm for a given space x and time t.  There are methods of modeling the composite temperature as a function of the matrix temperature only, but these require the use of mathematical techniques that are beyond my expertise.

And as a reward for having to bear with all these boring calculations...treat yourself with the edible and tasty version of our composite material.