Chapter 9: Section 4

Theory of the Thermal Conductivity of Liquids

Leo Peters

CENG 402 Project: April 26, 2002

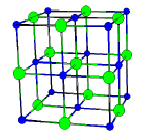
Even though a very detailed kinetic theory for the thermal conductivity of monatomic liquids was developed a half-century ago, means of implementing it for practical calculations have not been developed. Rough theories and empirical estimation methods are currently being employed to provide estimates of the thermal conductivity of monatomic liquids.

Bridgman's theory of energy transport in pure liquids is employed here in determining thermal conductivities. The following two assumptions were made:

  • The molecules are arranged in a cubic lattice, with a center-to-center spacing given by (Vn/Nn)^(1/3), in which Vn/Nn is the volume per molecule.
  • The energy is to be transferred from one lattice plane to the next at the sonic velocity Vs for the given fluid.

    • By rearranging the thermal conductivity from the rigid-sphere gas theory in Equation 9.3-11, the following equation is obtained.

    [Maple Math]

    Since the heat capacity at constant volume of a monatomic liquid is the same as for a solid at high temperature, the Dulong and Petit formula of Cv = 3(kappa/m) is applied. Better agreement is obtained for a lower coefficient, so 2.80 is normally used. The mean molecular speed in the y direction, Uy, is replaced by the sonic velocity Vs. The distance a that the energy travels between two successive collisions is taken to be the lattice spacing (Vn/Nn)^(1/3). These substitutions lead to a modified version of Bridgman's equation (Equation 9.4-3).

    [Maple Math]

    The velocity of low-frequency sound is given by the following equation (Equation 9.4-4).

    [Maple Math]

    Here Cp/Cv can be taken as nearly unity for liquids, except near the critical point. The remaining quantity can be determined from isothermal compressibility measurements.

    The following link provides an example on how to predict the thermal conductivity of a liquid.

  • Example 9.4-1

    • Here is a list of useful links.

  • Thermal Conductivity Conversion Factors

  • Thermal Conductivity and Thermal Properties

  • Thermal Conductivity of the Elements

  • Thermal Conductivity