Schmidt Number: Sc = mu/rho/DAB = viscosity/density/diffusivity
The Schmidt number, often abbreviated Sc, is a
dimensionless quantity with important applications to transport phenomena.
According to Bird, Stewart, and Lightfoot, "The Schmidt number is the ratio
of momentum diffusivity to mass diffusivity and represents the relative
ease of molecular momentum and mass transfer. It is analogous to
the Prandtl number, which represents the ratio of the momentum diffusivity
to the thermal
diffusivity" (BSL 600). The Schmidt number
becomes important in calculations of binary mass transfer between phases,
as demonstrated in Chapter 22 of our text.
While the CENG 402 class already has a Matlab
program, prcalc, to calculate the Prandtl number, no analogous program
existed for the purpose of determining the Schmidt number -- until now.
In April of 2002 we
unveil a nifty feat of engineering: not one,
but two Matlab programs which can be used to easily determine the Schmidt
number. The first, sccalc, calculates Sc for low density binary gas
mixtures, while scliqcalc determines Sc for dilute binary mixtures of several
common liquids. Both functions require the prior use of start301
to obtain the necessary data for the desired compounds. The contents
of the two Matlab m-files may be found below.
Also included are examples of their use and applications.
Matlab Program to Calculate Schmidt Number of Binary Gas Mixtures at Low Density
The Schmidt number appears most frequently in correlations used to calculate
mass transfer coefficients, which
can then be used to calculate such quantities as rate of evaporation.
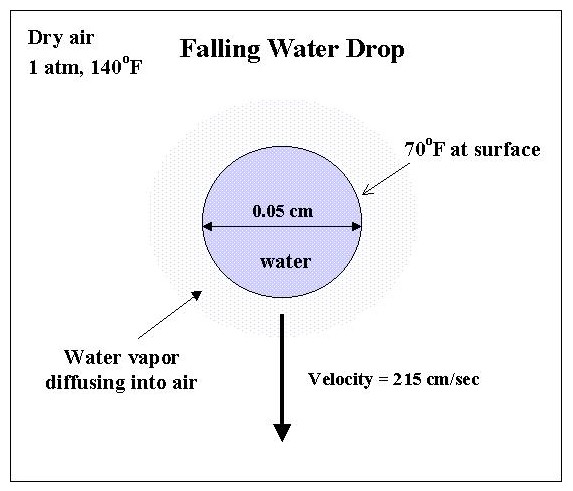
For instance, example 22.3-1 on
page 682 of the text (BSL) gives the following problem:
"A spherical drop of water, 0.05 cm in diameter, is falling at a velocity
of 215 cm/sec through dry, still air at 1
atm pressure with no internal circulation. Estimate the instantaneous
rate of evaporation from the drop, when the drop surface is at T0 = 70
degrees F and the air (far from the drop) is at Tinf = 140 degrees F.
The vapor
pressure of water at 70 degrees F is 0.0247 atm. Assume quasi-steady
state conditions."

The mass transfer coefficient can be found from the Sherwood number,
but to calculate that, we need the
Schmidt number! What if the problem didn't give the density,
viscosity, and diffusivity? Okay, so this
particular example does, but life is not always so simple. That's
where sccalc comes to the rescue. Here's
how it works:
______________________________________________________________________________
function sc = sccalc(p,T,zs,index)
% function sc = sccalc(p,T,zs,index)
%
% Calculates the Schmidt number for low density,
binary gas mixtures, using the Matlab functions
% mixmu and dcalc to calculate the viscosity
and diffusivity of the mixture, respectively.
%
% mixmu uses equations 1.4-15 and 1.4-16 in BS&L,
2nd ed to give viscosity mu in kg/m/sec
% dcalc uses the Chapman-Enskog formula to give
diffusivity DAB in m^2/sec
% Density rho is calculated using the ideal gas
law with a weighted average of the molecular weights
% of the two compounds. Units are kg/m^3.
%
% Argument List:
% p
[=] total pressure in atm
% T
[=] temperature in units of Tdeg, as specified using start301
% zs
[=] vector of mol fractions for the compounds
% index [=] indices of the compounds
from start301. If no
%
index vector is given, compounds 1 and 2 will be used.
% Returns:
% sc
[=] Schmidt number (unitless)
%
% Example: >> start301 (specify new session,
mass & energy balances, ceng301 database,
%
temperature in Kelvin, 2 compounds: chlorine and air)
%
>> Sc = sccalc(1,297,[0.25 0.75],[1 2])
%
%
DAB = 1.2015e-05
%
mu = 1.6407e-05
%
rho = 1.6183
%
Sc = 0.8439
%
% Created April 2002 by Danielle Dunn and Jessica
Dunn
global mw lenjones Tdeg
if nargin==3
index = [1 2];
end
pkPa = p*1.0133*10^2;
% dcalc requires pressure in kPa
DAB = dcalc(pkPa,T,index)
% DAB in units of m^2/sec
mu = mixmu(zs,T,index)
% mu in units of kg/m/sec
T = at(T); % converting temperature to K
j = index(1);
k = index(2);
mixmw = zs(1)*mw(j) + zs(2)*mw(k);
R = 0.08206;
rho = p*mixmw/R/T
% rho is in kg/m^3
sc = mu/rho/DAB;
____________________________________________________________________________________
So now let's see what this program can do! Back to example 22.3-1:
Using a pressure of 1 atm, the
film temperature of 105 degrees F, and the mole fraction of water in
the water/air mixture (given in the
problem as 0.0124), the Matlab program gives:
>> Sc = sccalc(1,105,[0.0124 1-0.0124])
DAB = 2.2951e-05 m^2/sec
mu = 1.8973e-05 kg/m/sec
rho = 1.1194 kg/m^3
Sc = 0.7385
From here, the Sherwood number, the mass transfer coefficient, and finally
the rate of evaporation can be
found as demonstrated in the example problem in the text.
The book gives a Schmidt number of 0.58. Notice that the density
and viscosity values given by Matlab
both compare very favorably to those given in the text on page 683.
The difference is in the calculation of
DAB. The text uses equation 17.2-1, based on kinetic
theory and corresponding states, while sccalc
references dcalc, which uses the Chapman-Enskog equation. Equation
17.2-1 is more accurate than Chapman-Enskog for polar compounds, such as
water in this case, but the opposite is true of nonpolar compounds.
The Chapman-Enskog equation is also less limited in the variety of systems
to which it can be applied.
Now consider a mixture of chlorine and air, two nonpolar substances.
Problem 17A.6 involves the calculation
of the Schmidt number for various mole fractions of chlorine in air.
Solution of BSL Problem 17A.6 (c): Calculation of
Schmidt Number for Chlorine in Air at 1 atm and 297 K
| Mole fraction of Cl2 |
|
|
|
|
|
| Sc from sccalc | 1.2828 | 0.8439 | 0.6100 | 0.4684 | 0.3752 |
| Sc from BSL | 1.27 | 0.832 | 0.602 | 0.463 | 0.372 |
It might also be informative to compare the results of our program to the experimental values provided in Table 17.1-1 of BSL:
Experimental and Sccalc Limiting Schmidt Numbers at 1 atm
| Sc from text | Sc from Matlab | Sc from text | Sc from Matlab | ||
| Gas Pair A-B | Temp (K) | xA->1 | xA->1 | xB->1 | xB->1 |
| H2-CH4 | 298.2 | 1.95 | 1.5207 | 0.23 | 0.2309 |
| H2-N2 | 273.2 | 1.40 | 1.4426 | 0.19 | 0.1996 |
| H2O-N2 | 308 | 0.58 | 0.6840 | 0.62 | 0.7398 |
Note that most of the sccalc values compare quite well to those from
the textbook, except for the water-nitrogen pair. The difference
again may be attributed to the fact that water is polar.
Matlab Program to Calculate Schmidt Number
of Dilute, Binary Liquid Mixtures
Well, we had created our sccalc program for calculating Sc for low
density gas mixtures. Still, something
seemed missing. What could it be? Then it hit us: liquids!
Liquids have Schmidt numbers, too! How
might we determine those?
In an effort to do so, we assembled our team of expert students.
Rebecca Sisson and Eric Lee provided the
liquid viscosity component, while Garrick Malone and Stanley Chan held
up their end of the bargain with a
liquid diffusivity algorithm. In the end, our collaborative efforts
led to a brand new program, fondly known
as scliqcalc, which may be used to determine the Schmidt number for
dilute, binary liquid mixtures. This
program will only work for the following compounds:
H2O water
C2H5C2H5O diethyl ether
C6H6 benzene
Br2 bromine
C2H5OH ethanol
H2SO4 sulfuric acid
CH2CH2 acetylene
HCl hydrogen chloride
NH3 ammonia
CHCl3 chloroform
CH3COOH acetic acid
CH2OHCH2OH ethylene glycol
C3H6 propylene
CH3COCH3 acetone
C3H8 propane
C6H5CH3 toluene
C6H5OH phenol
CCl4 carbon tetrachloride
The secret recipe is given below:
________________________________________________________________________________
function scliq = scliqcalc(T,zs,solvent,index)
% function scliq = scliqcalc(T,zs,solvent,index)
%
% Calculates the Schmidt number for dilute binary
mixtures of
% liquids, using the following:
%
% liqmucalc -- calculates the viscosity
of the solvent (the compound
%
with higher mole fraction) as an approximation to
%
the viscosity of the mixture. It is assumed that the dilute
%
solute contributes negligibly to the viscosity of
%
the mixture.
% ldiff code -- a modified version of the ldiff
program created by
%
Garrick Malone and Stanley Chan is included in our code.
%
This program uses the empirical Wilke-Chang equation, eq. 17.4-8 to
%
calculate the diffusivity for small concentrations
%
of solute A in solvent B.
%
% The density used in calculating the Schmidt
number is the density of the
% solvent at or near room temperature (it
is assumed that the
% dilute solute has negligible effect on
density of the mixture).
%
% Argument List:
%
% T
[=] temperature in units of Tdeg, as specified using start301
% zs [=]
vector of mole fractions for the two compounds
% solvent[=] association parameter
of solvent liquid species as follows
%
1 - 'water'
%
2- 'methanol'
%
3- 'ethanol'
%
4- 'propanol'
%
5- 'other' (other unassociated solvents)
% index [=] indices of the
compounds from start301. If no
%
index vector is given, compounds 1 and 2 will be
%
used.
%
% Returns:
% sc [=]
Schmidt number (unitless)
%
% Note: If the program returns NaN for the Schmidt
number, this
% means that the start301 database does not include
the necessary
% data for the compounds you chose.
%
%
Created April 2002 by Danielle Dunn and Jessica Dunn
global mw lenjones Tdeg lrho
if nargin==3
index = [1 2];
end
if zs(1)>zs(2)
k = index(1);
% k is the index of the solvent
j = index(2);
% j is the index of the solute
else
k = index(2);
j = index(1);
end
A= input('If you want to try to use the CENG301 data bank, type 1, otherwise type 2: ');
if A==1
VA=1/(lrho(j,2)/1000/mw(j));
% VA = molar volume of solute
else
VA=input('What is the molar volume of the solute in cm^3/g-mol:
');
end;
mu=liqmucalc(T,k);
% mu is in units of cp
T=at(T);
molwt=mw(k);
if solvent==1
psiB=2.26;
elseif solvent==2
psiB=1.9;
elseif solvent==3
psiB=1.5;
elseif solvent==4
psiB=1.2;
elseif solvent==5
psiB=1.0;
end;
DAB=(7.4E-8)*sqrt(psiB*molwt)*T/mu/(VA^.6)/(100^2) % m^2/sec Wilke-Chang equation
mu = mu*10^(-3) % mu is now in kg/m/sec
rho = lrho(k) % kg/m^3
scliq = mu/rho/DAB;
______________________________________________________________________________
In order to test the accuracy of our scliqcalc program, we located data
for viscosity, density, and diffusivity
for some common liquid pairs, using the CRC handbook*. From this
data, we calculated the Schmidt numbers
and compared them to those given by scliqcalc. The results are
shown below:
From start301:
Here are your compounds' formulae and names:
No. Formula Name
----------------------------------------
1 H2O water
2 C2H5OH ethanol
3 C6H5CH3 toluene
4 CH3COCH3 acetone
----------------------------------------
>> Sc = scliqcalc(25,[0.001 0.999],3,[1 2])
If you want to try to use the CENG301 data bank, type 1, otherwise
type 2: 1
DAB = 3.0324e-09 m^2/sec
mu = 0.0010 kg/m/sec
rho = 789 kg/m^3
Sc = 434.8772
for solute water, solvent ethanol
From CRC*, the density of ethanol at 20 deg C is 0.7893 g/cm^3, viscosity of ethanol at 25 deg C is 1.074 mPa*sec, and the DAB of infinitely dilute water-ethanol solution is 1.24*10^-5 cm^2/sec. This gives a Schmidt number of 1097.
>> Sc = scliqcalc(25,[0.001 0.999],5,[1 3])
If you want to try to use the CENG301 data bank,
type 1, otherwise type 2: 1
DAB = 6.6204e-09 m^2/sec
mu = 5.5031e-04
kg/m/sec
rho = 866
kg/m^3
Sc = 95.9847
for solute water, solvent toluene
From CRC, the density of toluene at 20 deg C is 0.8669 g/cm^3 and the viscosity at 25 deg C is 0.560 mPa*sec. The DAB of an infinitely dilute water-toluene solution at 25 deg C is 6.19*10^-5 cm^2/sec. This gives a Schmidt number of 104.4.
>> Sc = scliqcalc(25,[0.001 0.999],5,[1
4])
If you want to try to use the CENG301 data bank, type 1, otherwise
type 2: 1
DAB = 9.5753e-09 m^2/sec
mu = 3.0215e-04 kg/m/sec
rho = 791 kg/m^3
Sc =
39.8923 for solute water, solvent acetone
From CRC, the density of acetone at 20 deg C is
0.7899 g/cm^3 and the viscosity at 25 deg C is 0.306 mPa*sec. The
DAB of an infinitely dilute water-acetone solution at 25 deg C is 4.56*10^-5
cm^2/sec, which gives a Schmidt number of 84.95.
Notice that some results are more accurate than others. This could
be because of the psiB values used. In the
case of the water-toluene system, the psiB value used is 1.0.
The textbook (BSL) says that this value is good for benzene, and toluene
is a very similar compound chemically. However, the value of 1.0
is also used for other compounds for which more accurate values are not
available, as was the case with acetone. This could explain why the
results for acetone are not as good. We should also note that most
of the DAB values given by CRC "cannot be relied upon to better than 10%."
Our viscosity and density values appear to coincide very well with those
given by the CRC handbook.
* Source of data for comparison: CRC Handbook
of Chemistry and Physics, 75th edition. Editor-in-Chief David R. Lide.
Boca Raton: CRC Press, 1994.