Example 11.4-1: Steady-State
Forced-Convection Heat Transfer in Laminar Flow in a Circular Tube
Problem:
Show how to set up the equations for the problem considered in
section 10.8 - namely, that of finding the fluid temperature profiles for the
fully developed laminar flow in a tube.
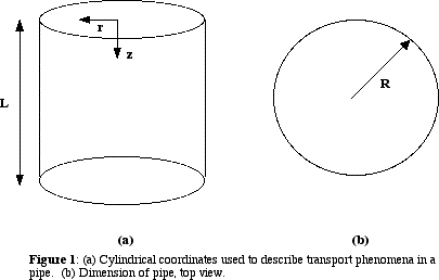
We will start with the general equations of continuity, motion,
and energy in cylindrical coordinates, make the necessary assumptions, and then
show that our result is that obtained in section 10.8.
> restart;
> s:=vector([r,Theta,z]); "S" is the position vector in cylindrical coordinates
![]()
> rho:=(s,t)->rho;
v:=vector([vr(r,Theta,z,t), vTheta(r,Theta,z,t), vz(r,Theta,z,t)]);
mu:=(s,t)->mu; The assumption is made that the fluid has
constant properties, i.e., constant density and constant viscosity;
Furthermore, velocity has three components, each of which can depend on space
and time.
![]()
![]()
![]()
> d[r]:=f->diff(f,r);
d[Theta]:=f->diff(f,Theta); d[z]:=f->diff(f,z); d[t]:=f->diff(f,t); These functions represent the differential operators in space and
time.
![]()
![]()
![]()
![]()
> d1:=d[r](v[1]): d2:=d[Theta](v[2]):
d3:=d[z](v[3]): d1,d2, and d3 represent the derivatives of
each velocity component with respect to its direction, e.g., the derivative
with respect to r of vr.
> continuity:=d[t](rho(s,t))+rho(s,t)*((1/r)*d[r](r*v[1])+(1/r)*d2+d3);
General equation of continuity for
cylindrical coordinates, expanded, with the assumption of constant physical
properties, as given in Appendix B, eq. B.4-2 in B,S,&L.
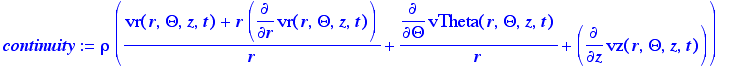
> motion:=rho(s,t)*(d[t](v[3])+v[1]*d[r](v[3])+(v[2]/r)*d[Theta](v[3])+v[3]*d3)+d[z](P(r,Theta,z,t))-mu(s,t)*((1/r)*d[r](r*d[r](v[3]))+(1/r^2)*d[Theta](d[Theta](v[3]))+d[z](d3));
General equation of motion in cylindrical
coordinates, as given in Appendix B, eq. B.6-6, assuming constant physical
properties. Gravitational term rho*gz(z) is combined with the pressure term
d(p(z))/dz by the term P(z), which is P =p(z)-rho*g*z,
a convenient way to sum the gravitational and pressure terms in balances.
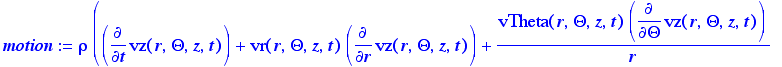
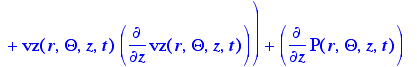
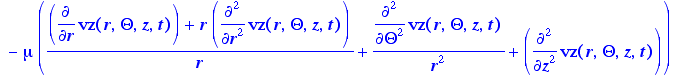
> energy:=rho(s,t)*Cp*(d[t](T(r,Theta,z,t))+v[1]*d[r](T(r,Theta,z,t))+v[2]/r*d[Theta](T(r,Theta,z,t))+v[3]*d[z](T(r,Theta,z,t)))-k*((1/r)*d[r](r*d[r](T(r,Theta,z,t)))+(1/r^2)*d[Theta](d[Theta](T(r,Theta,z,t)))+d[z](d[z](T(r,Theta,z,t))))-mu(s,t)*Phi(r,Theta,z,t);
General energy equation, expanded,
assuming constant physical properties, as given in Appendix B, eq. B.9-2
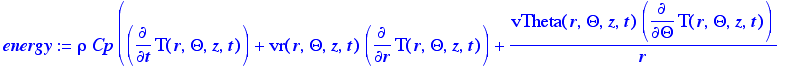
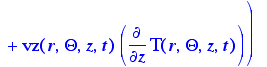
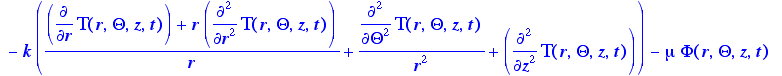
> Phi:=(r,Theta,z,t)->2*(d1)^2+2*(d2/r+v[1]/r)^2+2*(d3^2)+(r*d[r](v[2]/r)+(1/r)*d[Theta](v[1]))^2
+((1/r)*d[Theta](v[3])+d[z](v[2]))^2+(d[z](v[1])+d[r](v[3]))^2-(2/3)*((1/r)*d[r](r*v[1])+(1/r)*d2+d3)^2:
> Phi(r,Theta,z,t); Phi is the equation for the general dissipation function in
cylindrical coordinates, as given in Appendix B by eq. B.8-2.
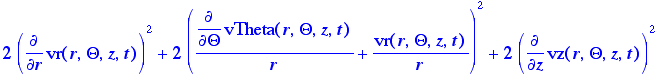
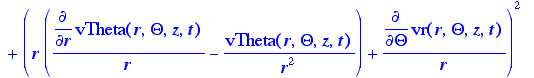
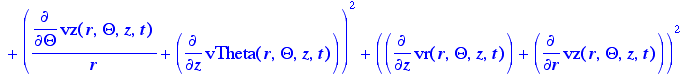
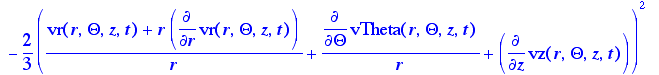
> rho:='rho': vr:='vr': vTheta:='vTheta':
vz:='vz': p:='p': T:='T': mu:='mu': We
need to free up these variable names so we can assign them again as functions
to simplify our equations of continuity,motion, and energy.
We now make some assumptions to reduce these general equations. We
want to assume that the only velocity component is in the z-direction, and that
it varies only with radial position. We also assume that pressure varies only
with height. Furthermore, we assume that the temperature T varies only with
height and radial position:
> vr(r,Theta,z,t):=0:
vTheta(r,Theta,z,t):=0: vz(r,Theta,z,t):=vz(r): T(r,Theta,z,t):=T(r,z):
P(r,Theta,z,t):=P(z): mu(r,Theta,z,t):=mu:
> continuity; Eq. 11.4-1
![]()
> motion; Eq. 11.4-2, with the derivative of r*dvz/dr expanded.
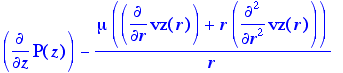
> energy; Eq. 11.4-3, with the term which contains a second derivative of T
expanded.
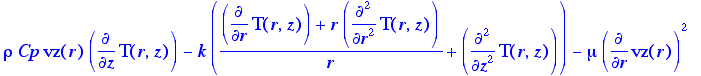
Next, we need to solve for the velocity distribution from the
equation of motion.
> sol:=dsolve(motion,vz(r));
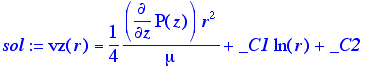
In order that the velocity be finite at r=0, the constant _C1 must
be 0 to prevent the natural log term from blowing up:
> _C1:=0; sol;
![]()
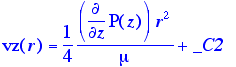
> assign(sol); vzr:=unapply(vz(r),r);
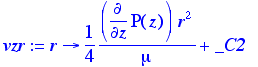
In order to solve for the last constant, we use the Boundary
Condition that at the pipe edge, the velocity is zero:
> bc2:=vzr(R)=0;
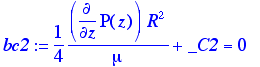
> _C2:=solve(bc2,_C2); Solve for the constant.
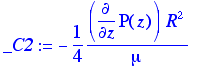
> simplify(vzr(r));
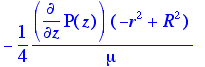
Pressure varies with height in a hydrostatic manner, and the
gravitational force varies monotonically with height: i.e., the derivative of P with respect to z the for the length of the pipe is simply
-(P(0)-P(L))/L
> eqP:=diff(P(z),z)=-(P0-PL)/L:
> sol:=dsolve(eqP,P(z)):
> assign(sol): P:=unapply(P(z),z): vzr(r);
![]()
This is the parabolic velocity distribution expected, as used in
section 10.8 as Eq. 10.8-1.
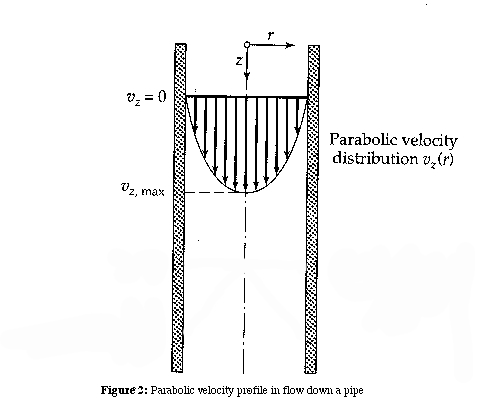
We now want to substitute this result into the energy equation.
But first, we need to make some assumptions about the equation of
energy: i) heat conduction in the z-direction is much smaller than heat
convection, so that we may neglect the second order differential of T, and ii)
the viscous heating effects are minimal, so that we may ignore the
mu*(d^2(vz)/dr^2) term:
> newenergy:=simplify(rho*Cp*vzr(r)*d[z](T(r,z))=k*(1/r)*d[r](r*d[r](T(r,z))));
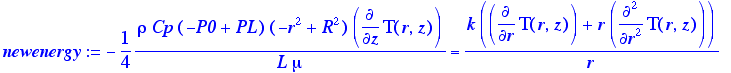
we will define vzmax as in eq. 2.3-19:
> mu:=(P0-PL)*R^2/4/L/vzmax:
simplify(newenergy);
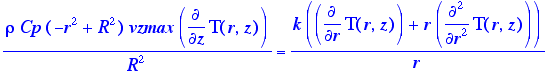
Comparing this result with the equation 10.8-12:
> eq10812:=rho*Cp*vzmax*(1-(r^2/R^2))*d[z](T(r,z))=k*((1/r)*d[r](r*d[r](T(r,z))));
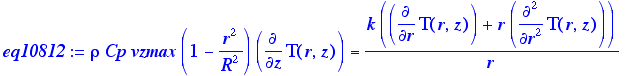
> difference:=simplify(eq10812-newenergy);
![]()
Thus, using the equations of motion to solve for the velocity
distribution in the fully developed laminar region region, we get the same
results as with the shell balance method.