
Theory of Diffusion in Colloidal Suspensions
(Section 17.5)
Background Information:
Colloidal suspensions are dispersions of small particles, ranging in size from 1 nanometer to 1 micrometer, in a solvent. The following image shows a colloid suspension of coenzyme 10:

Colloidal suspensions differ from solutions in that the substance used as a solute is appreciably larger than the solute of a solution, as the photo shows. In addition, the components are mixed manually since physical interactions are not strong enough to cause the solute to dissolve. A phenomenon known as Brownian motion keeps the particles suspended in the solvent. Brownian motion is the constant bombardment of the colloid particles by the solvent molecules. This action prevents the colloid particles from settling out of the solvent. More importantly, Brownian motion contributes to the diffusion of colloid particles through the solution. In 1905, Albert Einstein investigated this phenomenon and derived a general expression for the diffusivity of colloid particles in solvents. This derivation differs significantly from that given by Bird, Stewart, and Lightfoot, but the end result is the same.
Derivation of Diffusivity:
Suppose a colloidal suspension is contained in a cylinder with a unit cross-sectional area as the following figure shows:

Diffusion of the colloid particles is occurring throughout the entire length of the cylinder. Let’s examine a small volume element of the cylinder, dx. Pressure is being applied on the volume element at x and x+dx. The net pressure in the positive direction can be given by:
![]()
This pressure is equivalent to the osmotic pressure. If this net pressure is divided by the length of the volume element, dx, the result is the net force on the element per unit volume, K:
![]()
In the limit that the volume element has an infinitesimal length, dx--> 0 and:
![]()
The osmotic pressure is given by the van’t Hoff equation:
![]()
where c is the concentration of the solute in the solvent, R is the gas constant, and T is the absolute temperature of the solution. Due to diffusion in the cylinder, the concentration of the solute depends upon the position, x. Differentiating the van’t Hoff equation with respect to x gives:
![]()
The osmotic pressure force will impart a velocity on the volume element. Since the colloid particles are fairly large, they will experience a drag force, decreasing their velocity. Assuming that the colloid particles can be modeled as hard spheres of a set radius, the velocity of the suspension is scaled by the Stokes friction coefficient:
![]()
where mu is the viscosity of the solvent and Ra is the radius of the colloid spheres. This leads to an expression for the velocity of the solution per unit volume:
![]()
This expression applies to the entire volume element, so it must be divided by the number of particles in the volume element to be applicable to a single particle:
![]()
If each side of the equation is divided by the concentration gradient term, the resulting equation gives the expression for the diffusivity:
![]()
If the Boltzmann constant is defined as R/N, the expression is identical to that given by Bird, Stewart, and Lightfoot in Eqn. 17.5-4:
![]()
Using this equation, the diffusivity of any colloidal suspension can be determined if the temperature of the suspension, viscosity of the solvent, and radius of the colloid particle are known as the following example shows.
Numerical Example:
Determine the diffusivity of a suspension of water and coenzyme 10 at 20 C. Assume that the average radius of a coenzyme 10 particle is 75 nm.
Solution: Maple can be used to easily solve this problem
The diffusivity of the colloidal suspension is given by the Einstein equation derived above
![]()
Define the known constants in the equation
> k:=1.38066e-16*erg/K; T:=293.15*K; Ra:=75*nm;
![]()
![]()
![]()
The viscosity of water at 20 C is given in Table 1.1-2 in BSL
![]()
Evaluate Dab
![]()
Now convert all units to C.G.S. units
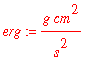
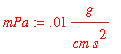
![]()
Now evaluate Dab again with all units converted
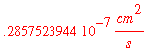
This answer is reasonable for a colloidal suspension because the size of the colloid particles results in a small flux, as the small value of the diffusivity indicates.