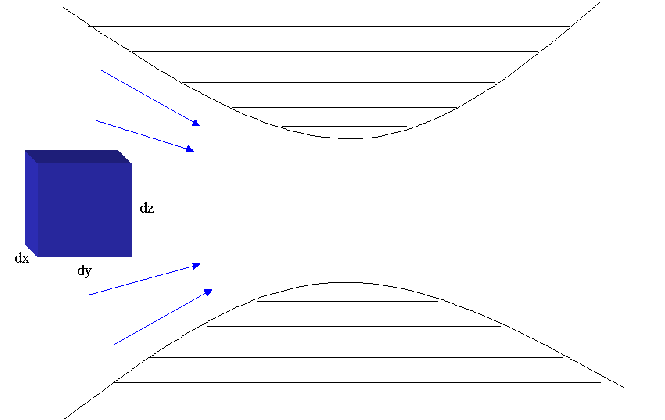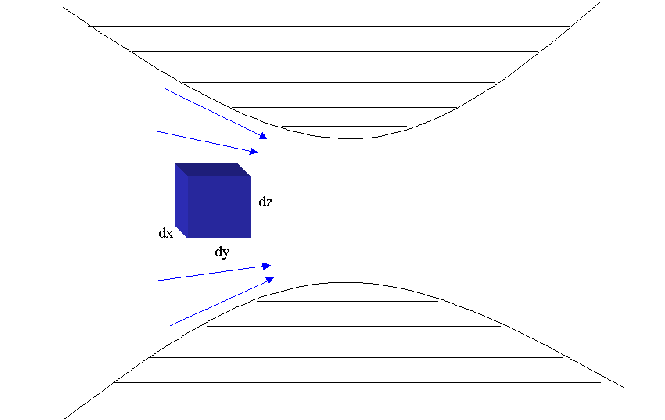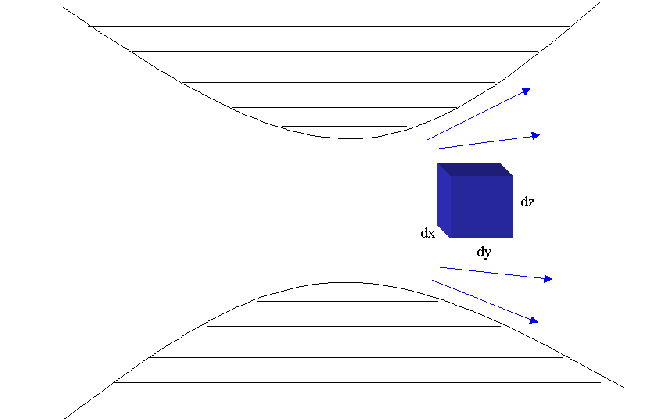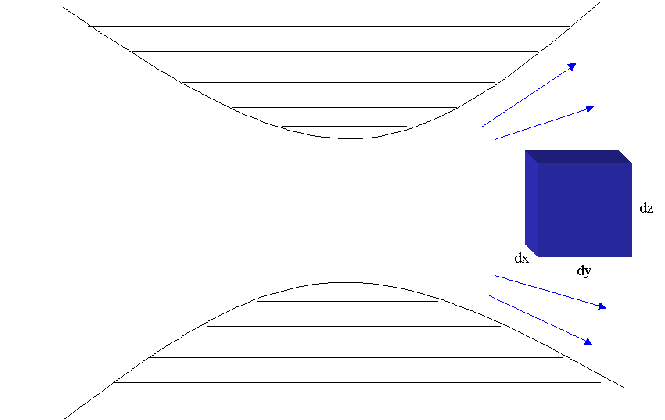
The diagram belows shows the movement of an element of a fluid moving
through a converging/diverging nozzle. The fluid is adiabatically
compressed through the center of the nozzle and then expands back out
adiabatically.

The resulting equations can be derived using two methods. The
following equations are derived using the equation of energy. They
can also be derived using the first law of
thermodynamics. Click here
to
see
this derivation.
>
restart;
>
with(linalg):
Define vectors to be used in expressions for the substantial time derivative and the total time derivative.
>
v:=(x,y,z)->vector([vx(x,y,z),vy(x,y,z),vz(x,y,z)]):
>
d_dt:=(x,y,z)->vector([dx_dt(x,y,z),dy_dt(x,y,z),dz_dt(x,y,z)]):
>
s:=vector([x,y,z]):
>
Vmass:=T->R*T/P/M;
The ideal gas law
>
DT_Dt:=(diff(T(t,x,y,z),t)+multiply(v(x,y,z),grad(T(t,x,y,z),s)));
The substantial time derivative for temperature.
>
DP_Dt:=(diff(P(t,x,y,z),t)+multiply(v(x,y,z),grad(P(t,x,y,z),s)));
The substantial time derivative for pressure.
>
eqnenergy:=rho*Cpmass*DT_Dt=T/Vmass(T)*D(Vmass)(T)*DP_Dt;
The equation of energy in the form presented in Table 10.4-1, eqn. J. It is assumed that the momentum flux and the heat flux are both negligible. Therefore, both those terms drop out of the equation. D(lnVmass)(lnT) at constant P is written here as D(Vmass)(T) * T/Vmass because Maple will not take the derivative of a natural log in terms of another natural log. Notice that this term is 1 for an ideal gas.
>
dT_dt:=(diff(T(t,x,y,z),t)+multiply(d_dt(x,y,z),grad(T(t,x,y,z),s)));
The total time derivative for temperature.
>
dP_dt:=(diff(P(t,x,y,z),t)+multiply(d_dt(x,y,z),grad(P(t,x,y,z),s)));
The total time derivative for pressure.
>
dx_dt(x,y,z):=vx(x,y,z): dy_dt(x,y,z):=vy(x,y,z): dz_dt(x,y,z):=vz(x,y,z):
dx_dt, etc. are the components of the velocity of the point of view that is taken in the total time derivative. If we are to follow the motion of an element of the moving fluid, then the dx_dt would equal vx, the corresponding component of the local fluid velocity. See the discussion of the different time derivatives on pg. 73 of BSL.
>
difference:=dP_dt/dT_dt-DP_Dt/DT_Dt;
For each element of the moving fluid the ratio of the total time derivatives minus the ratio of the substantial time derivatives is zero. Therefore, DP_Dt/DT_Dt=dP/dT.
>
eqnnew:=rho*Cpmass=D(P)(T);
The new energy equation making the adjustments discussed above.
>
rho:=P(T)*M/R/T;
The ideal gas law where rho=1/Vmass
>
eqnnew;
Substituting for rho gives eqn. 10.5-72 in the text.
>
Cpmass:=gamma*Cvmass; R:=(Cpmass-Cvmass)*M;
The first equation is the definition of gamma. The second is the relationship between Cp and Cv for an ideal gas.
>
simplify(eqnnew);
Substituting in for Cpmass gives eqn. 10.5-73. Here, d(lnP)/d(lnT) is written as D(P)(T)*T/P.
>
sol:=dsolve(eqnnew, P(T));
Solve for P(T)
>
C1:=solve(subs(P(T)=P,sol),_C1);
Solve for the constant (renamed C1). P was substituted for P(T) so that a substitution for T could later be made without confusing Maple.
>
C2:=simplify(C1^((gamma-1)/gamma),assume=positive);
Assuming gamma is constant, then C1 raised to the (gamma-1)/gamma power will also yield a constant (C2). This gives eqn. 10.5-74 in text.
>
unassign('R'); unassign('rho'); T:=P*M/rho/R;
R and rho need to be cleared so that they can be used in the definition of T. T is defined using the ideal gas law.
>
C3:=simplify(C2*M/R);
Both M and R are constants, so multiplying C2 by M and dividing by R will yield another constant (C3).
>
C4:=simplify(C3^(-gamma), assume=positive);
Again, gamma is assumed to be constant. Therefore, C3 raised to the -gamma power will yield yet another constant (C4). Keep in mind that none of these constants are equal. This gives eqn. 10.5-75 in the text.
An ideal gas at 5 bars and 500 degrees Farenheit
flows through an ideal turbine (reversible and adiabatic) and exits at a
pressure of 1 bar. What is the temperature of the exiting gas?
>
restart;
>
C3:=P^((gam-1)/gam)/T;
Same equation as derived above
>
C3prime:=subs({P=P1,T=T1},C3);
The same equation but rename P and T so that it can be applied at the second state. C3prime is equal to C3.
>
P1:=1*bar;
Define P1 using the ideal gas law.
>
P:=5*bar;
Define P2 using the ideal gas law.
>
T1:=solve(C3=C3prime,T1);
Set C3 equal to C3prime and solve for the second temperature, T1
>
T:=(300+459.67)*degR;
Given in the problem
>
gam:=1.4;
Given in the problem
>
evalf(T1);
evaluate T1
>
Warning, new definition for norm
Warning, new definition for trace
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![[Maple Math]](images/project22.gif)
![[Maple Math]](images/project23.gif)
![[Maple Math]](images/project24.gif)
![]()
![[Maple Math]](images/project26.gif)
![]()
![[Maple Math]](images/project28.gif)
![[Maple Math]](images/project29.gif)
![]()
![]()
![[Maple Math]](images/project32.gif)
![]()
![]()
![]()