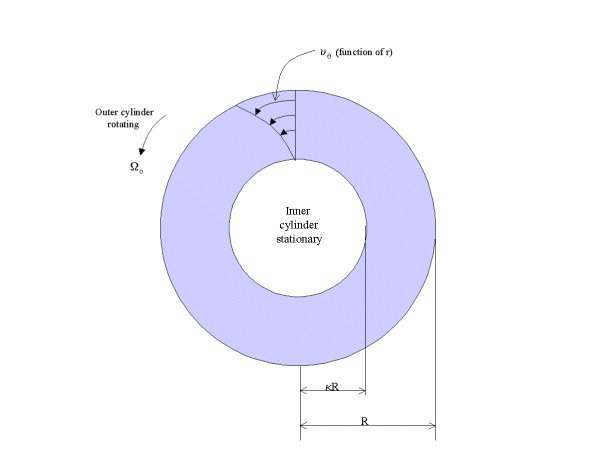
Example 10.5-1. Tangential Flow in an Annulus with Viscous Heat Generation.

This example illustrates a forced-convection problem, where we determine the temperature distribution in an incompressible Newtonian fluid held between two coaxial cylinders.

> restart;

> conteqn:=diff(1/r*diff(r*vt(r),r),r)=0; Continuity equation for the theta-component (cylindrical coordinates).

> dsolve({conteqn,vt(kappa*R)=-Omega*kappa*R,vt(R)=0},vt(r)): Solve for velocity (theta-component).

> simplify(%);

> diff(%/r,r): Use the result in second term of Eqn 10.5-5.

> simplify(%);

> Dvel:=-2*Omega*kappa^2*R^2/(r^3*(kappa^2-1)); Define second part of the above equality.

> tde:=mu*(r*Dvel)^2; Second term in Eqn 10.5-6.

> de:=k*diff(r*diff(T(r),r),r)/r + tde;

> tr:={r=xi*R,T=Tk+Theta*(T1-Tk)};

> with(PDEtools,dchange);

> newde:=dchange(tr,R^2*de/(k*(T1-Tk)),[xi,Theta(xi)]);

> mu:=N*k*(1-kappa^2)^2*(T1-Tk)/(Omega^2*R^2*kappa^4);

> eqn:=simplify(newde);

> s:=dsolve({eqn,Theta(kappa)=0,Theta(1)=1},Theta(xi)); solving the DE and inserting the B. C. 10.5-12&13.

> assign(s);

> Theta:=unapply(Theta(xi),xi):

> simplify(Theta(xi),xi); Compare with Eqn 10.5-14.

Without the dimensionless quantities, the differential equation looks like this:

> restart;

> Dvel:=-2*Omega*kappa^2*R^2/(r^3*(kappa^2-1)):

> eqn5_6:=k*1/r*diff(r*diff(T(r),r),r)+mu*(r*Dvel)^2=0; Compare with Eqn 10.5-6.

> tp:=dsolve({eqn5_6,T(kappa*R)=Tk,T(R)=T1},T(r)): Used to solve sample problems.

>

Sample Problems:

The first one illustrates a case where a maximum temperature is reached.

A maximum temperature is reached when the Brinkman number is large enough (hence the dimensionless variable N is also large enough). This second sample problem illustrates another case where a maximum temperature is reached, but the space between the cylinders is much smaller.

Since the cylinders are so close together, as they are in the second sample problem, the equation found in Chapter 9.4 is capable of providing a fairly accurate answer. Otherwise, the temperature distributions that the equation yields (for large area between cylinders) is not at all accurate. The results of the second sample problem using this method can be found here.

The third sample problem illustrates the case where there is no maximum temperature between the cylinders.