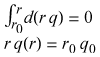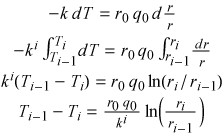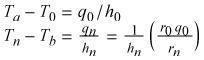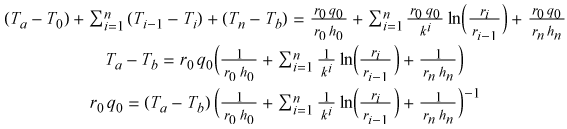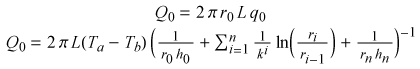Heat Conduction Through
Composite Cylindrical Walls:
CENG 402 Project

This page created by Dave Smith 4/25/99.
Email question/comments to dsmith@rice.edu.

        Introduction
        Problem Description
        Defining Parameters and Variables
        The Shell Energy Balance
        Solving the Energy Balance
        Calculating Q₀ = q₀ A₀

Introduction

This page discusses and solves the problem of heat conduction through a cylindrical pipe insulated with several layers of mateials, each of a different thickness and with a different thermal conductivity. This problem is also discussed as Example 9.6-1 of Transport Phenomena by Bird, Stewart, and Lightfoot.

Note: all of the work shown in the problem solution below was evaluated in Mathematica. To download the complete Mathematica notebook created for this problem, click on ceng402_ex9.6-1.nb.

Problem Description

In industry, the most common method used to transport fluids between units and around the plant is to pump the fluid through a cylindrical pipe. In most cases, it is desired to keep the fluid at some temperature either above or below the ambient air temperature. Hence, to minimize heat flux into or out of the pipe, the pipe is covered with insulation. The insulation may be composed of several different layers, each layer having a different thicknesses and a different thermal conductivity. Given (a) the temperature of the fluid inside the pipe, (b) the ambient temperature outside, (c) information about the thickness and thermal conductivity of each layer of insulation, and (d) the heat transfer coefficients at the fluid-pipe and insulation-air interfaces, derive an expression for the heat flux per unit length of pipe across the pipe.

Defining Parameters and Variables

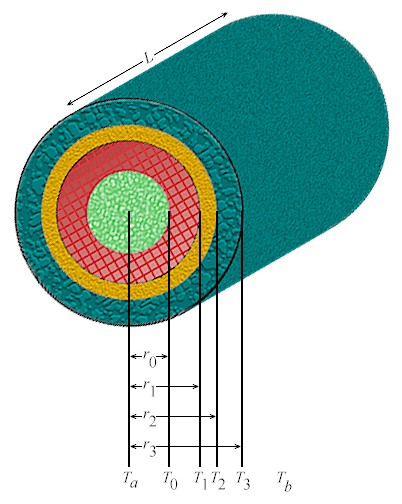
As shown in the diagram, the cylinder is of length L. The fluid inside the pipe is at temperature T_a and occupies a cylindrical space of radius r₀. At r₀ the inner pipe wall is at temperature T₀ and the heat-transfer coefficient between the fluid and the wall is h₀. The i^th layer of insulation extends from radius r_i-1 to r_i. At radial position r_i the insulation is at temperature T_i. The outermost insulation layer, the n^th layer, is at temperature T_n, extends to r_n, and has a heat-transfer coefficient h_n with the outside air. The air is at temperature T_b. The heat flux q out of the tube and the per unit length heat flow Q / L depend on the above parameters.

The Shell Energy Balance

In its most general form, the balance equation over some control volume CV states that for every transportable quantity Z, the rate of accumulation of Z inside CV equals the net rate of flux of Z into CV plus the rate of formation of Z inside CV. In this problem, the quantity being transported is heat energy, no heat is being generated anywhere throughout the tube, and at steady-state there is no heat accumulation. Thus, we have

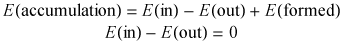
The heat flux q measures the per unit time per unit area flow of heat. Therefore, taking the control volume as the radial shell from radius r to r+dr,

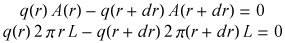
Solving the Energy Balance

Dividing the shell balance equation through by 2 pi L dr (the volume of this shell),

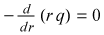
Integrating with respect to r from r = r₀ to r, and using the boundary condition that q = q₀ at r = r₀,

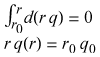
Applying Fouier's Law,

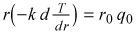
Separating variables and integrating,

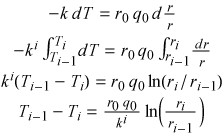
Note that the thermal conductivity of the i^th layer of insulation (the region from r = r_i-1 to r = r_i) is denoted as kⁱ. Finally, Newton's Law of Cooling defines the heat-transfer coefficient at the two pipe-fluid interfaces: q = h (T₂ - T₁), where q and (T₂ - T₁) have the same sign. Therefore,

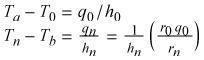
Calculating Q₀ = q₀ A₀

Adding the above three equations,

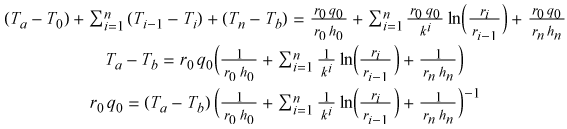
Defining the total heat flow through the pipe as Q₀ = q₀ A₀,

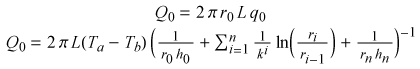
The last equation is an expression for the total heat flow out of the tube. All quantities in the expression are assumed to be known or easily measurable: the length of the tube, the temperature of both the fluid and the ambient air, the two heat-transfer coefficients, and the thicknesses and thermal conductivities of the insulation layers.

This page created by Dave Smith 4/25/99.
Email question/comments to dsmith@rice.edu.