Example 17.4-1
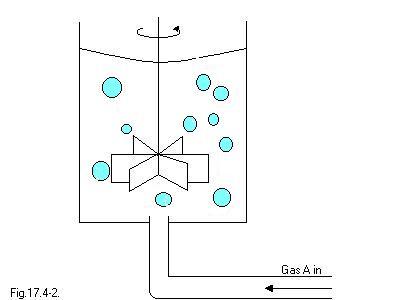
Example 17.4-1

In order to do this problem we must make the following assumptions:
a.) Each gas bubble is surrounded by a stagnant liquid film of thickness delta, which is small with respect to the bubble diameter.
b) A steady-state concentration is quickly established in the liquid film after the bubble if formed.
c) The gas A is only sparingly soluble in the liquid, so that we can neglect the bulk flow term in Eq. 17.0-1.
d) The bulk of the liquid outside the stagnant film is at concentration cA delta, which changes so slowly with respect to time that it can be considered to be constant.
Eq. 17.0-1;
> N[Az]:=-c*D[AB]*diff(x[A](z),z)+x[A]*(N[AZ]+N[Bz]);
Is now reduced to
> N[Az]:=z->-DAB*D(cA)(z);
By performing a mass balance
through a differential segment ![]() z we get
:
z we get
:
> eq:=-limit((N[Az](z)-N[Az](z+dz))/dz,dz=0)+k1*cA(z)=0;
Now we apply the boundary conditions and solve for cA(z);
B.C. 1 at z = 0, ![]() =
= ![]()
B.C. 2 at z = ![]()
![]()
> s:=dsolve({eq,cA(0)=cA0,cA(delta)=cAdelta},cA(z)); Finding a solution for Ca and making Ca a function of z
![]()
![[Maple Math]](images/proj12.gif)
> assign(s);cA:=unapply(cA(z),z);
![]()
![[Maple Math]](images/proj14.gif)
Next we change our variables to simplify our expressions, and make cA a function of zeta;
> z:=zeta*delta;cAdelta:=cA0*Gamma;k1:=b1^2*DAB/delta^2;assume(b1>0);assume(delta>0);assume(zeta>0); Changing variables to make expressions look less complicated
![]()
![[Maple Math]](images/proj17.gif)
>
C[A]:=zeta->simplify(convert(cA(z),trig));
It's more convenient to have Ca as a function
of ![]() instead of z
instead of z
> C[A](zeta);
![]()
![]()
![]()
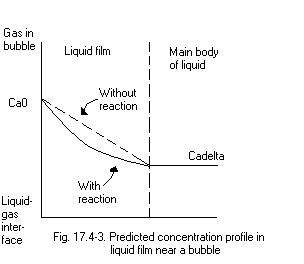
In the case of no chemical reaction;
> eq13:=(c[A]/cA0)=limit(C[A](zeta)/cA0,b1=0): I took the limit because substituting 0 for b1 gives a division by zero error.
> solve(eq13,{c[A]/cA0});
![[Maple Math]](images/proj25.gif)
The mass fluxes for absorption with and without reaction are;
>
N[Az]='N[Az]':
I had to define ![]() as a variable, since I already used it at the
beginning, so that I could redefine it here
as a variable, since I already used it at the
beginning, so that I could redefine it here
>
k:=(-DAB*diff(C[A](zeta),zeta))/delta;
This is Eq. 17.4-14. I divided it by delta
because I'm taking the derivative with respect t ![]() . According to the chain rule d(Ca)
/d z
= d(Ca)/d
. According to the chain rule d(Ca)
/d z
= d(Ca)/d ![]() * d
* d ![]() /dz
/dz
![]()
![]()
>
N[Az]:=unapply(k,zeta);
Making ![]() a function of
a function of ![]()
![]()
![]()
>
N[Az](0);
Setting ![]() = 0, because z = 0, to obtain
Eq.17.4-14
= 0, because z = 0, to obtain
Eq.17.4-14
![[Maple Math]](images/proj37.gif)
>
c[A]:=solve(eq13,c[A]);
Obtaining ![]() from eq13, which is a few lines
above
from eq13, which is a few lines
above
> N[Aznorxn]:=(-DAB*diff(c[A],zeta))/delta; Eq. 17.4-15
To obtain eq 17.4-16;
>
Gamma:=0:N[Aznorxn];
![]() =0 in eq. (17.4-15) but not in eq.
(17.4-14)
=0 in eq. (17.4-15) but not in eq.
(17.4-14)
> Gamma:='Gamma':
Defining ![]() as a variable, so that the previous definition
of
as a variable, so that the previous definition
of ![]() doesn't affect the
doesn't affect the ![]() in Eq.17.4-14
in Eq.17.4-14
> Nstr:=N[Az](0)/(DAB*cA0/delta); Eq. 17.4-16
![[Maple Math]](images/proj48.gif)
To obtain eq. (17.4-18) we must
evaluate d ![]() /dz at z =
/dz at z =
![]() and, because of B.C.
2, set eq. (17.4-12) equal to
and, because of B.C.
2, set eq. (17.4-12) equal to
![]()
> eq2:=C[A](zeta)=cAdelta; Substituting cAdelta for cA in Eq. 17.4-12
![]()
![]()
![]()
> Cad:=solve(eq2,cAdelta);
I defined cAdelta as cA0
![]() above, so this command just solves eq2 for cA0
above, so this command just solves eq2 for cA0
![]() , a quanitty that I chose to call Cad
, a quanitty that I chose to call Cad
![]()
![]()
![]()
Next we must equate the mass of A crossing the outer surface of the film with the amount of A being removed by chemical reaction in the bulk of the liquid;
> eq3:=-A*DAB*(diff(Cad,zeta)/delta)=V*k1*cAdelta; Eq. (17.4-17)
![]()
![[Maple Math]](images/proj63.gif)
> funct:=unapply(eq3,zeta);
Changing eq3 to funct(
![]() ) so that I can evaluate it at
) so that I can evaluate it at
![]() = 1
= 1
![]()
![[Maple Math]](images/proj67.gif)
> funct(1);
at z = ![]() ,
, ![]() = 1
= 1
![[Maple Math]](images/proj70.gif)
> gama:=solve(funct(1),Gamma); Eq. 17.4-18
![[Maple Math]](images/proj71.gif)
> Gamma:=gama;
Using the above solution to define
![]()
![[Maple Math]](images/proj76.gif)
> fnleq:=simplify(Nstr); Eq.17.4-19
![[Maple Math]](images/proj78.gif)
In order to create the plot of N* vs. b1 I used the books expression for Eq. 17.4-19, because Maple would not rearrange my expression so that I could substitute different values for V/Adelta.
> restart;
> Nbk:=(b1/sinh(b1))*(cosh(b1)-1/(cosh(b1)+b1*(alpha)*sinh(b1))); I substituted alpha for (V/Adelta)
![[Maple Math]](images/proj82.gif)
> alpha:=0:
> p1:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5): This command just saves a bunch of numbers in p1, that are displayed later on
> alpha:=10^2:
> p2:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5):
> alpha:=10^4:
> p3:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5):
> alpha:=10^6:
> p4:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5):
> alpha:=10^8:
> p5:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5):
> alpha:=10^100:
> p6:=loglogplot(Nbk,b1=.1e-3..10,y=.8..1.5):
> with('plots'): This allows you to make log-log plots and do about a million other cool things with graphs
> display([p1,p2,p3,p4,p5,p6]);
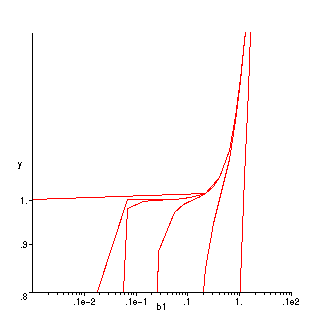
This plot does is almost like the one in the book except for the seemingly straight lines. I think that the lines are not as curvy because I made the plot on log-log scale.
Find the ratio of the absorption rate with a first-order reaction to the absorption rate with a zero order reaction, i.e. no reaction, using the following data:
V = 100 m^3, A = 1 m^2, delta = 1 m
> restart;
>Nstar:=(b1*(b1*sinh(b1)*cosh(b1)*V+A*delta*(cosh(b1))^2A*delta))/(A*sinh(b1)*delta*cosh(b1)+V*b1*(cosh(b1))^2-V*b1);
![[Maple Math]](images/proj171.gif)
> b1:=.8;V:=100;delta:=1;A:=1;
![]()
![]()
![]()
> Nstar;