This example shows how to use the relationship obtained to solve problem 18.C in Bird, Stewart, and Lightfoot. In this example, the concentration of the A component (albumin) is so small that we assume the concentration of the B component (water) to be constant (ie- xB = xB0). This simplification allows for an analytical solution to equation 18.5-18, and thus MAPLE can easily be used to solve for the concentration profile of albumin.

Data Given

centrifugal field = 50,000 times force of gravity

cell length = 1.0 cm

molecular weight of albumin (component A) = 45,000

apparent density of albumin in solution = M_A/V_A = 1.34 g/cm³

mole fraction of albumin at z = 0, x_A0 = 5x10^-6

apparent density of water in then solution = 1.00 g/cm³

temperature = 75^oF

MAPLE solution

> restart;

> eq:=(xA(z)/xA0)^VBbar=exp((VAbar*MB-VBbar*MA)*gom*z/(R*T));

> xA(z):=solve(eq,xA(z)):xA:=unapply(xA(z),z);

> coef:=(VAbar*MB-VBbar*MA)*gom/(VBbar*R*T);

> MA:=45000*g/mol:

> MB:=18*g/mol:

> VAbar:=MA/rhoA:

> rhoA:=1.34*g/cm^3:

> VBbar:=MB/rhoB:

> rhoB:=g/cm^3:

> T:=(75+460)/1.8*K:

> R:=8.314e7*g*cm^2/(s^2*mol*K):

> gom:=50000*980.665*cm/s^2:

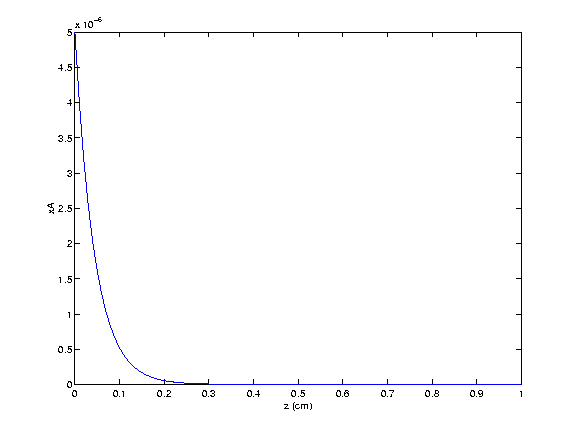
> xA0:=5e-6:xA(z);

This is the same result that BSL obtained for the concentration profile.