COMPOSITE CYLINDRICAL WALLS

CENG 402

APRIL 2001

This is a modified example problem from Transport Phenomena by Bird, Stewart and Lightfoot.

Chapter 9 - Example 9.6-1

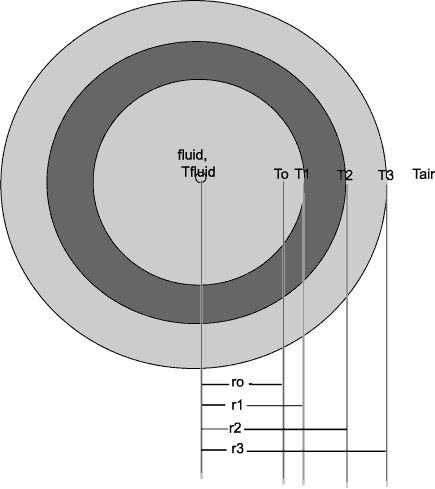
Model the above cylindrical pipe using thermal energy balances. The thermal conductivities of the three regions of pipe are k1, k2, and k3.

Heat transfer coefficients are given by hin and hout, denoting the coefficients at the product-inner radius and outer radius-air interface respectively.

See BS&L example 9.6-1 for additional details.

> restart;

Start with a shell of unspecified boundary temps and radii.

> Area := r -> 2*Pi*r*L;

Energy balance gives {Thermal Energy In} - {Thermal Energy Out} + {Thermal Energy Formed} = 0

> Q := (r) -> q(r) * Area(r);

> EnBal := Q(r) - Q(r+dr);

Consider division by 2*pi*L*dr, with limit dr -> 0

> Eq := limit ( EnBal / (2*Pi*L*dr) , dr = 0 );

> Deq := 0 = Eq;

This, of course, is equivalent to d(r*q)/dr. Define q(ro) = qo.

> eq := dsolve( { Deq, q(ro) = qo } , q(r) );

Note that q(r) is the heat flux through any region, as we defined earlire a generic shell only.

Now we consider Fourier's law of heat conduction:

> q(r) := -k * D(T)(r);

Substitute into the existing equation for q(r).

> eq;

Here we have seperated variables and integrate from the inner to outer interface of each region.

> LHS := int( -k , T = Tin ... Tout);

> RHS := int(rhs(eq),r = rin ... rout);

> region := LHS = RHS;

This expression holds for every region in which there is no fluid-solid interface.

In cases of fluid-solid interface (inner surface, outer surface), we will use Newton's law of cooling to model the heat transfer.

> q := h*(T - Tfliud);

The results can now be generalized, for N layers. Here we will solve a situation analogous to the book, with three insulation types.

The inner and outer layers will be modeled using Newton's law of cooling.

> T := array(0...3): r := array(0...3): k := array(0...3): expr := array(0...4):

> for i from 0 to 2 by 1 do

> expr[i+1] := T[i] - T[i+1] = qo * ro / k[i+1] * ln( r[i+1] / r[i] )

> od;

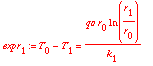
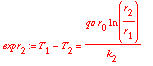
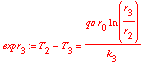
Properties of the logarithm were used -> log(A) - log(B) = log(A/B)

Now define the first and last expressions for heat transfer - at the fluid - solid interfaces.

> expr[0] := qo = hin*(Tfluid - T[0]);

> expr[4] := qo*r[0]/r[3] = hout*(T[3] - Tair);

Now solve for Qo, the overall heat transfer.

> S := 0;

> S := sum(expr[j] , j = 0 ... 4);

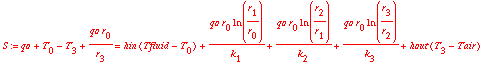
We now want to solve for qo, from which Qo can be determined.

> q0 := solve (S,qo);

This value multiplied by the surface area gives the total heat flow, Qo.

> Qo := q0 * Area( r[0] );

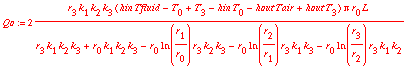
Define over-all heat transfer coefficient based on inner surface :

> Uo := Qo / (Area(r[0])) / (Tfluid - Tair);

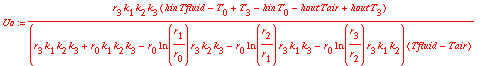
PRACTICE WITH A CALCULATOR.

EXAMPLE PROBLEMS - ALUMINIUM, COPPER AND CAST IRON TUBES

We here consider the implications of various types of material with respect to the pipe size and temp distribution.

Data was taken from Shaumes, Outline for Heat Transport. Thermal conductivities were given over three temperature regions.

We assume them to be constant over those regions.

Inner Pipe Diameter = 2.54 cm

Thickness = 0.635 cm

Tfluid = 1000C Tair = 50C

T1 = 500C T2 = 300C

 FOR ALUMINUM:

Inner Pipe Diameter = 2.54 cm

Thickness = 0.635 cm

> r[0] := 2.54*cm: r[1] := r[0]+0.635*cm:

> hin := 0.27*cal/cm^2/sec/K: hout := 1.27*cal/cm^2/sec/K:

> Tfluid := (1000+273.15)*K: Tair := (50+273.15)*K:

> T[1] := (500+273)*K: T[2] := (300+273.15)*K:

> k[1] := .645*cal/sec/cm/K: k[2] := .540*cal/sec/cm/K: k[3] := .492*cal/sec/cm/K:

> expr[0]; expr[1];

> solve( {expr[0] , expr[1]} , {T[0] , qo} );

> T[0] := 868.91*K; qo := 109.14*cal/cm^2/sec;

> expr[2];

> r[2] := solve(expr[2] , r[2]);

> expr[3]; expr[4];

> solve({ expr[3] , expr[4]} , { r[3] , T[3] });

Thus we have accounted for all variables - clearly the second expressoin for T3, r3 does not hold.

>

> restart;

FOR COPPER

> r[0] := 2.54*cm: r[1] := r[0]+0.635*cm:

> hin := 0.27*cal/cm^2/sec/K: hout := 1.27*cal/cm^2/sec/K:

> Tfluid := (1000+273.15)*K: Tair := (50+273.15)*K:

> T[1] := (500+273)*K: T[2] := (300+273.15)*K:

> k[1] := .856*cal/sec/cm/K: k[2] := .876*cal/sec/cm/K: k[3] := .901*cal/sec/cm/K:

> solve( {expr[0] , expr[1]} , {T[0] , qo} );

> T[0] := 848.85*K; qo := 114.56*cal/cm^2/sec;

> r[2] := solve(expr[2] , r[2]);

> solve({ expr[3] , expr[4]} , { r[3] , T[3] });

>

>

>

> restart;

FOR CAST IRON

> r[0] := 2.54*cm: r[1] := r[0]+0.635*cm:

> Tfluid := (1000+273.15)*K: Tair := (50+273.15)*K:

> hin := 0.27*cal/cm^2/sec/K: hout := 1.27*cal/cm^2/sec/K:

> T[1] := (500+273)*K: T[2] := (300+273.15)*K:

> k[1] := .103*cal/sec/cm/K: k[2] := .114*cal/sec/cm/K: k[3] := .131*cal/sec/cm/K:

> solve( {expr[0] , expr[1]} , {T[0] , qo} );

> T[0] := 1071.94*K; qo := 54.33*cal/cm^2/sec;

> r[2] := solve(expr[2] , r[2]);

> solve({ expr[3] , expr[4]} , { r[3] , T[3] });

Angela Thomas-Strayhorn

Steve "the phenomena" Abel